AI Innovations and Insights 23: KAG, AlphaMath, and Offloading

This article is the 23rd in this compelling series. Today, we will explore three intriguing topics in AI, which are:

• KAG: Brilliant Detective Who Masters Evidence and Connects the Dots

• AlphaMath: The Brilliance of AlphaGo's Insights in LLM Reasoning

• LLM Inference: Offloading

Exquisite Video Imagery:

KAG: Brilliant Detective Who Masters Evidence and Connects the Dots

Open-source code: https://github.com/OpenSPG/KAG

Vivid Description

KAG is like a smart detective who can both analyze evidence (knowledge graphs) and integrate clues (text retrieval).

When faced with a complex case, he follows multiple leads in his reasoning, eliminates irrelevant information, and ultimately pieces together the complete truth. He can quickly navigate through professional domains like healthcare, solving challenges and providing convincing conclusions.

Overview

Existing RAG systems face three major challenges: they rely too heavily on text or vector similarity for retrieval, lack sufficient logical reasoning or numerical capabilities, and require extensive professional knowledge.

KAG improves the effectiveness of LLMs in professional fields by combining the reasoning power of knowledge graphs with the generative capabilities of LLMs.

Figure 1: The KAG Framework. The left side shows KAG-Builder, while the right side displays KAG-Solver. The gray area at the bottom of the image represents KAG-Model. [Source].

As shown in Figure 1, the KAG framework consists of three components:

• KAG-Builder focuses on building offline indexes. It features a Knowledge Representation framework that is friendly to LLMs and supports mutual indexing between knowledge structures and text chunks.

• KAG-Solver introduces a Logical-form-guided hybrid reasoning solver, combining LLM reasoning, knowledge reasoning, and mathematical logic. It also uses semantic reasoning for knowledge alignment, enhancing the accuracy of representation and retrieval in both KAG-Builder and KAG-Solver.

• KAG-Model optimizes the capabilities of each module based on a general language model.

Since it integrates knowledge graphs, KAG essentially involves two main steps: building the knowledge graph and using it for question answering.

First, let’s look at how the knowledge graph is built.

Figure 2: The Pipeline of KAG Builder for domain unstructured documents. [Source].

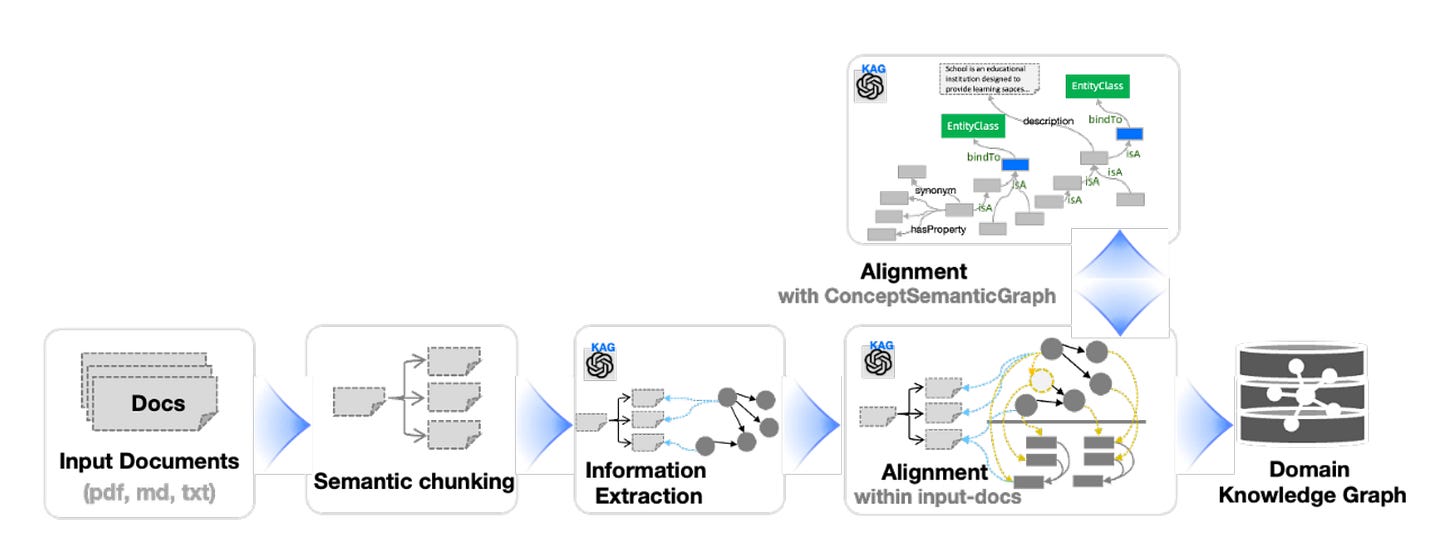
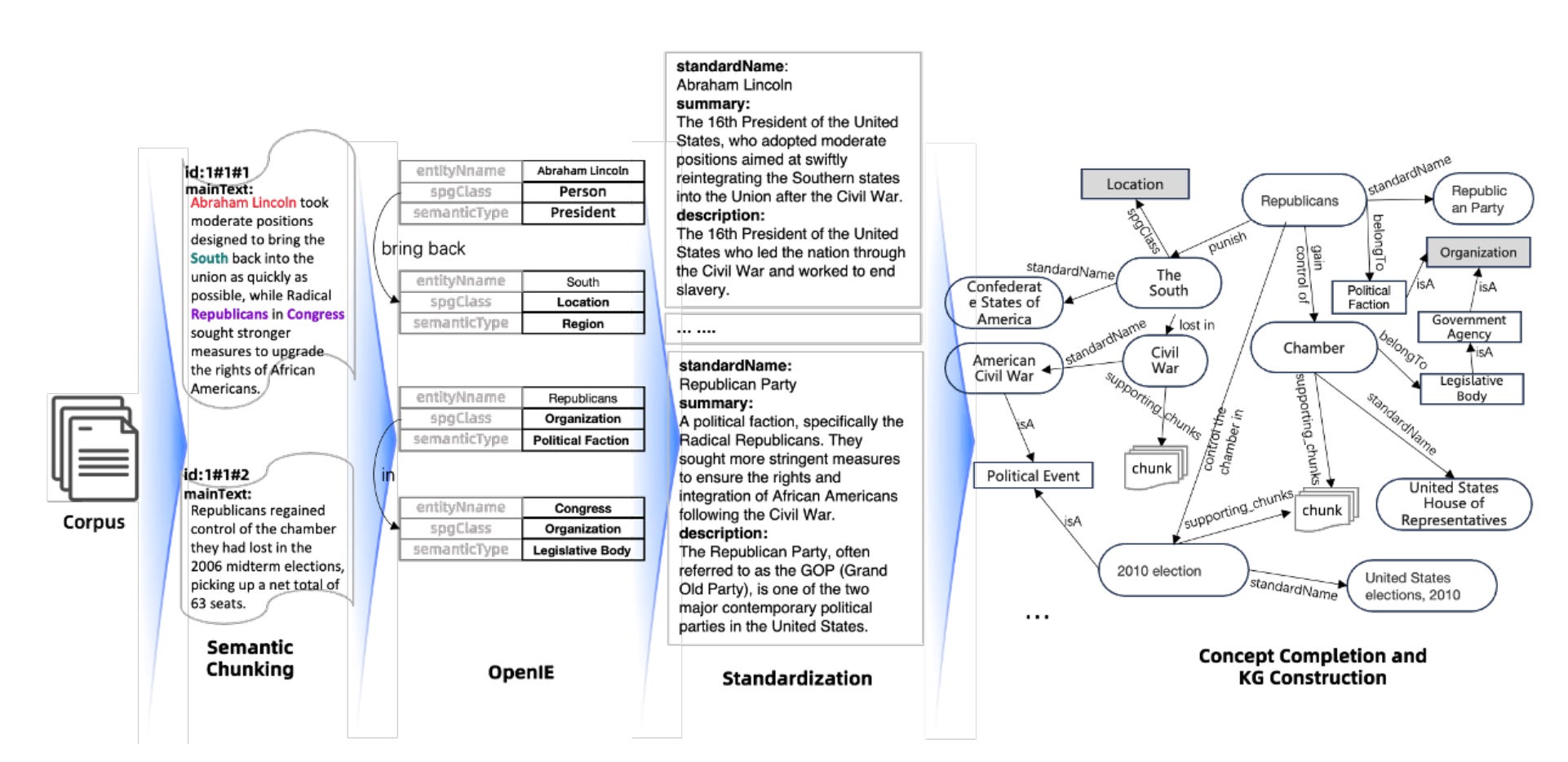
As shown in Figure 2, first, phrases and triples are extracted through information processing. Then, disambiguation and fusion are performed using semantic alignment. Finally, the constructed knowledge graph is stored.

Figure 3 shows an Example of KAG-Builder pipeline.

Figure 3: An Example of KAG-Builder pipeline. [Source].

After building the knowledge graph, how can we use it to answer a query?

Figure 4: An Example of logical form execution. [Source].

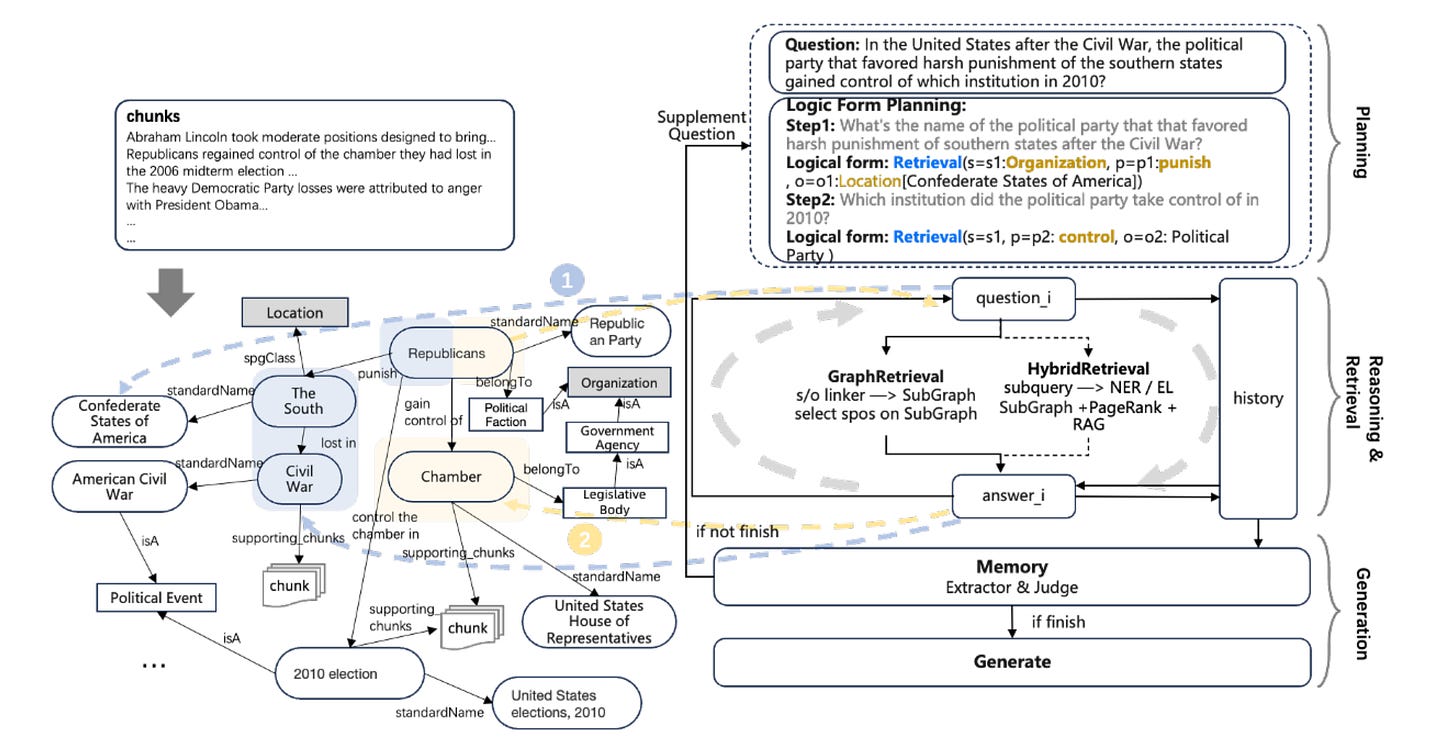
The right part of Figure 4 illustrates the reasoning and iteration process. First, the user's question undergoes logical form decomposition. Then, logical-form-guided reasoning is used for retrieval and reasoning. Finally, the generation module determines whether the user's question is satisfied. If the answer isn’t satisfactory, a new question is provided to repeat the decomposition and reasoning process. Once the answer meets the criteria, the generation module outputs the final response.

Commentary

I have the following insights:

• KAG addresses RAG's semantic limitations by connecting entities in knowledge graphs, creating meaningful links between information.

• While KAG excels at complex reasoning tasks, RAG performs faster for simple information retrieval. KAG is most valuable in professional domains (such as healthcare) where deep understanding is crucial, combining domain knowledge graphs with advanced reasoning.

• GraphRAG uses modularity-based algorithms (like Leiden) to detect communities, enabling query-focused summarization. Meanwhile, KAG builds cross-references between text data and knowledge graphs, leveraging logical-form hybrid reasoning. GraphRAG is ideal for summarizing large-scale content, like news articles, by extracting global themes and trends. KAG works best for specialized Q&A systems, such as e-government or e-health, where precise and logically sound answers are essential.

AlphaMath: The Brilliance of AlphaGo's Insights in LLM Reasoning

Open-source code: https://github.com/MARIO-Math-Reasoning/Super_MARIO

Vivid Description

Imagine a math teacher who not only provides solutions but also explores multiple ways to approach a problem. When given a question, instead of immediately answering, they think through it from scratch (MCTS), considering various strategies (Policy Model). As they work, they record each step, scoring themselves for correct steps (Value Model) and deducting points for mistakes (Backpropagation). After each problem, they reflect on their process and refine their approach. Over time, through continuous practice, they get better at solving complex problems.

This is how AlphaMath works—by generating reasoning paths and learning from self-feedback to improve problem-solving skills.

Overview

Improving large language models' reasoning capabilities, particularly in mathematics, has always been a research hotspot.

One effective method relies on domain experts or GPT-4 to obtain large amounts of high-quality process supervision data (i.e., solution processes) for fine-tuning, artificially injecting external knowledge into LLMs, but this is not only costly but also labor-intensive.

AlphaMath is a novel approach that combines pretrained LLMs with a carefully designed Monte Carlo Tree Search (MCTS) framework. This combination enables LLMs to autonomously generate high-quality mathematical reasoning solutions without requiring professional human annotations.

Figure 5: AlphaMath involves iterating through three distinct stages. [Source].

As shown in Figure 5, AlphaMath involves iterative training:

• Collect a dataset of mathematical questions and their correct answers.

• Use MCTS on the policy and the value model to generate both correct and incorrect solution paths, along with state values.

• Optimize the policy and value model using the data generated from MCTS.

What are the policy model and value model? The policy model is an LLM with an added tanh-activated linear layer acting as a value model, alongside the standard softmax layer for token prediction (Figure 5, right). This architecture allows the two models to share most parameters.

Figure 6: An overview of the four key operations in MCTS. [Source].

As shown in Figure 6, AlphaMath's MCTS process is actually quite similar to AlphaGo (Zero), for example, the selection process uses a variant of the PUCT algorithm:

After obtaining the trained model, MCTS can be used for inference.

MCTS is computationally demanding and challenging for production use. AlphaMath simplifies this by removing the backpropagation step and introducing Step-level Beam Search (SBS), which selects optimal child nodes dynamically instead of constructing a full tree. SBS offers two key improvements: introducing a beam width to limit node expansions, and using value model predictions directly instead of Q-values from multiple simulations.

Commentary

AlphaMath is innovative and has shown encouraging results in mathematical reasoning, but in my view, there is still room for improvement.

• Error correction mechanism: It lacks a clear algorithm for detecting and correcting faulty reasoning in real-time. Without proper error detection, mistakes at one step can cascade through the solution process. In longer reasoning chains, these compounding errors could significantly impact the final result.

• The experimental data currently focuses on mathematical problems. Questions remain about effectively transferring AlphaMath to other domains requiring multi-step reasoning.

LLM Inference: Offloading

In the previous article, we discussed an overview of LLM Inference, including optimization measures at three levels: Data-Level, Model-Level, and System-Level.

Today we'll introduce a popular field, Offloading, which is actually part of the Inference Engine under System-Level Optimization.

Vivid Description

Imagine an athlete training in a gym. He has a lot of equipment (GPU’s storage and computational tasks), but not all of it is used at all times. Some equipment (weights) is not needed during certain phases of his training, so the athlete can move it to a less busy room (CPU). This way, the athlete can focus on other tasks that require more immediate attention, avoiding an overload of equipment on the main training floor.

Overview

Offloading explores ways to offload tasks from GPUs to CPUs to better manage memory usage and computational efficiency for LLMs in resource-constrained environments. Some representative techniques include:

1. FlexGen: Offloads weights, activations, and KV cache to CPU while optimizing throughput through graph traversal. It also overlaps data loading and storing to further boost efficiency.

2. llama.cpp: Offloads computation to the CPU to reduce data transfer overhead, though at the cost of low-powered CPU.

3. Powerinfer: Utilizes activation sparsity by offloading "cold" neurons (less frequently computed) to the CPU, improving efficiency with sparse operators and predictors.

4. FastDecode: Offloads both storage and computation of the attention operation to the CPU, reducing data transfer and minimizing pipeline inefficiencies.

Commentary

Overall, offloading is indeed an intuitive approach. The goal is to optimize GPU and CPU workloads to improve memory usage and computational throughput for LLMs.

I'm just starting to learn about this field, and I'll share more insights when I have them.

---

Finally, if you’re interested in the series, feel free to check out my other articles.