This article is the 25th in this profound series. Today, we will explore two intriguing topics in AI, which are:
rStar-Math: The AlphaGo of Mathematics
Probing-RAG: A Smart Chef
rStar-Math: The AlphaGo of Mathematics
Open-source code: https://github.com/microsoft/rStar
In the previous article, we explored the principles of rStar. Recently, the rStar series recently updated rStar-math.
Vivid Description
rStar-Math is like the AlphaGo of mathematics.
Just as AlphaGo used Monte Carlo Tree Search (MCTS) and deep learning to surpass human players, rStar-Math applies MCTS to explore mathematical solutions step by step, with a Process Preference Model (PPM) to evaluate the quality of each move.
The key difference? AlphaGo operates within the fixed rules of Go, while rStar-Math navigates the vast, ever-changing landscape of mathematical problems. It’s more than just a calculator—it’s a problem solver that continuously improves, like a strategist in the world of mathematics.
Overview
rStar-Math stands out by matching and even surpassing OpenAI o1 in mathematical reasoning—all without distilling knowledge from more advanced LLMs. It achieves this with just two small language models (SLMs).

As shown in Figure 1, rStar-Math introduces a self-evolutionary method for math problem-solving through three key innovations:
A novel code-augmented CoT data synthesis method: Uses Monte Carlo Tree Search (MCTS) rollouts to generate verified reasoning steps, ensuring correctness by executing corresponding Python code and discarding invalid steps. Q-values are assigned to each intermediate reasoning step, measuring their contribution to correct answers, thereby improving trajectory quality.
A Process Preference Model (PPM) training approach: Learns to score reasoning steps based on preference pairs derived from Q-values, rather than using them directly, to avoid noisy and imprecise stepwise rewards. The PPM uses a pairwise ranking loss to distinguish between correct and incorrect steps, leading to more reliable training signals compared to conventional Q-value-based methods.
A four-round self-evolutionary process: Starts with a dataset of 747k math word problems, iteratively improving the policy model and PPM. Each round refines the system by generating progressively higher-quality reasoning trajectories, leading to a stronger policy model, more reliable PPM, and better training data. The improved training data allows the model to solve increasingly complex and even competition-level math problems, demonstrating significant generalization.
By combining MCTS, preference-based learning, and iterative self-improvement, rStar-Math establishes a scalable, self-improving method for mathematical reasoning, paving the way for autonomous evolution in structured problem-solving AI.
Commentary
With just two SLMs (1.5B or 7B—a policy SLM and a PRM) and 4×A100 (40GB) GPUs, rStar-Math delivers impressive results. This demonstrates that MCTS is practical and not constrained by heavy resource requirements.
Traditional MCTS approaches rely solely on MCTS rollout evaluations, often leading to incorrect reasoning paths, reward errors, or poor search quality. Improving the Process Reward Model (PRM) is key to overcoming these issues. rStar-Math enhances PRM accuracy with three key strategies:
Converting reasoning paths into code and verifying them through execution.
Introducing a Process Preference Model (PPM) to assess reasoning quality using positive and negative samples.
By combining MCTS with a PPM, it goes beyond traditional rollout methods, making it better suited for complex mathematical reasoning.
In my view, rStar-Math has the potential to become a key reference for the MCTS approach in the field of large-scale reasoning. It shows that small language models (SLMs) + efficient search (MCTS) + precise rewards (PPM) = effective mathematical reasoning.
But I have some concerns:
rStar-Math uses MCTS to calculate Q-values (step quality scores), but these values are still based on post-hoc estimates from search trajectories. This doesn’t necessarily guarantee an accurate reflection of the reasoning process.
Can the MCTS + PPM approach be applied beyond math reasoning? Mathematical problems can be verified through code execution (e.g., Python calculations), but language-based reasoning lacks a clear validation mechanism.
Probing-RAG: A Smart Chef
Vivid Description
Imagine a chef preparing a meal.
A typical chef (Traditional RAG) might go to the grocery store before cooking—every single time—without checking what’s already in the fridge. This wastes time and could lead to unnecessary or incorrect purchases (redundant retrieval).
Probing-RAG, on the other hand, works like a smart chef. Before heading out, it opens the fridge (checks the LLM’s internal knowledge) to see if all the necessary ingredients are already available. If everything is there, it starts cooking right away (generates an answer). But if something is missing—say, garlic—it only then makes a quick trip to the store (retrieves external information).
This approach saves time and ensures the dish is complete without unnecessary steps or missing key ingredients.
Overview
Traditional RAG may not be optimized for real-world scenarios, where queries might require multiple retrieval steps or, in some cases, no retrieval at all.
Adaptive-RAG is a typical example of an adaptive retrieval approach, which classifies queries into three categories based on their complexity: no retrieval needed, single-step retrieval, or multi-step retrieval.

However, as shown on the left side of Figure 2, the external classifier in Adaptive-RAG often fails to fully leverage the internal decision-making capabilities of the language model. This results in unnecessary retrieval steps and conflicts between the model's internal knowledge and external retrieval information.
Probing-RAG, on the other hand, assesses whether the language model needs to retrieve documents by probing its internal representations. As illustrated on the right side of Figure 2, Probing-RAG focuses on the hidden states of the LLM’s intermediate layers. These hidden states serve as inputs to a "prober," which evaluates whether further retrieval steps are necessary.
Essentially, the prober checks if the LLM can generate an answer based solely on the available information. It is built by adding a fully connected layer to the LLM, with a parameter size of only 5 MB, which is 2000 times smaller than the external classifier-based Adaptive-RAG.
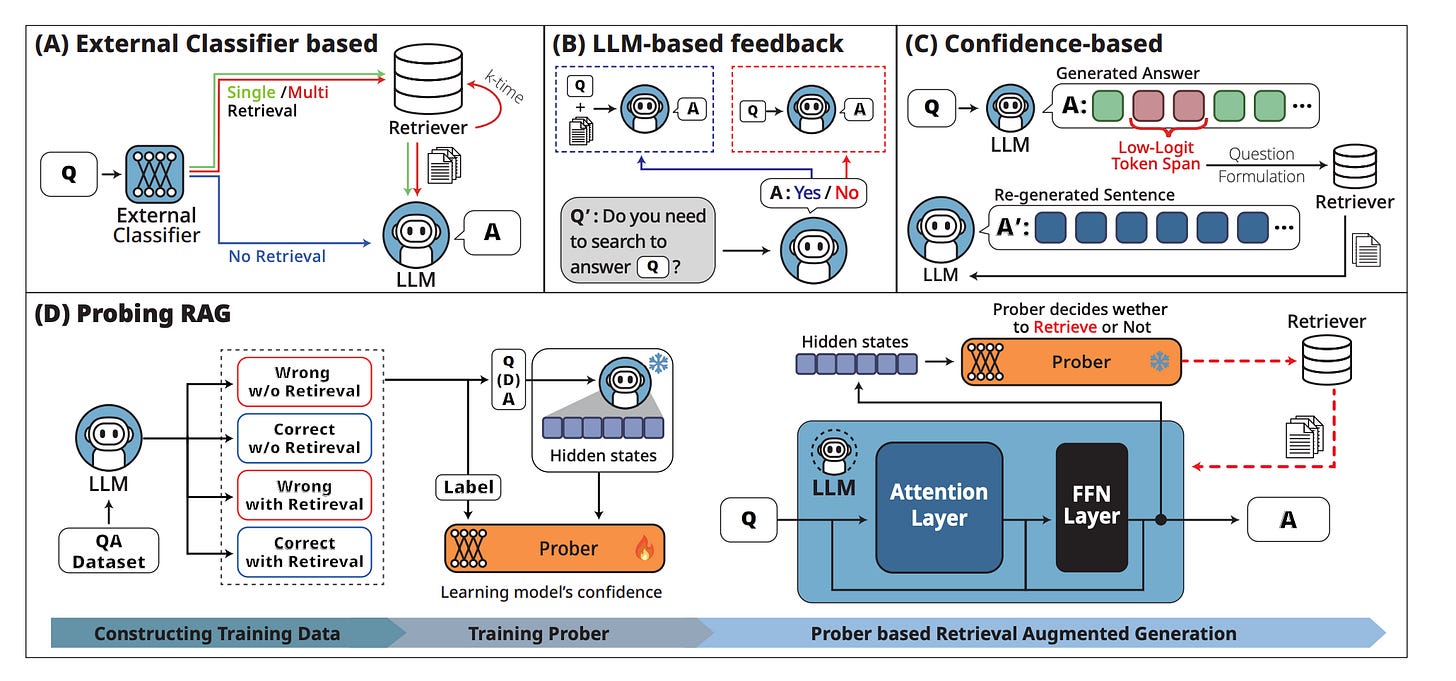
Traditional adaptive retrieval methods can generally be categorized into three main approaches:
External classifier-based: Figure 3 (A) determines whether retrieval is needed based on query complexity, as assessed by an external classifier.
LLM feedback-based: Figure 3 (B) decides retrieval based on the response from the LLM.
Confidence-based techniques: Figure 3 (C) uses the confidence level of the final token selection to determine whether retrieval is necessary.
Figure 3 (D) illustrates Probing-RAG, which decides retrieval using a prober model that leverages the LLM's internal hidden states.
To train the prober, positive and negative samples are generated with cross-entropy loss used for optimization.
In the RAG process, the LLM generates updated answers in each iteration, using retrieved documents until no further retrieval is needed or the maximum iterations are reached.
Commentary
Overall, Probing-RAG's key contribution is its ability to determine whether external retrieval is needed by analyzing the LLM's hidden states. This reduces unnecessary retrieval and lowers computational costs.
But I have a few concerns and questions.
Limited Representation Power: The Prober relies on a single-layer fully connected network. In deep learning, such networks have limited representation capacity and may struggle to capture the complex reasoning patterns within an LLM.
Scalability Across Different LLMs: Probing-RAG trains the Prober on hidden states from layers 6–14 of Gemma-2B. However, LLMs of different sizes (e.g., 7B, 13B, 70B) have varying numbers of layers and different patterns of hidden state evolution. Can this Prober be applied to larger or smaller models? Would it need retraining for each LLM? In addition, it only works with open-source LLMs, making it incompatible with closed-source models.
Simplistic Data Labeling: The Prober's training data is labeled based on LLM-generated answers: retrieval is not needed (y=1) if the answer is correct, and needed (y=0) if the answer is incorrect. However, this binary labeling approach may oversimplify the decision-making process, overlooking nuances between partial retrieval and no retrieval:
Case 1: The LLM may partially know the answer but lack certain details. If it provides an incorrect response, it may not be due to a complete lack of knowledge but rather missing specific information.
Case 2: The LLM might generate a correct answer based on faulty reasoning. In this case, the Prober could mistakenly classify it as "no retrieval needed," leading to cascading errors.
Finally, if you’re interested in the series, feel free to check out my other articles.



