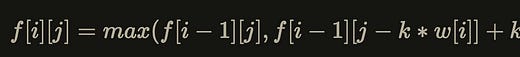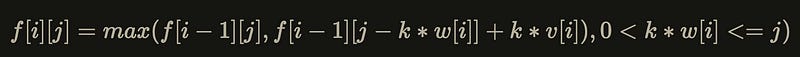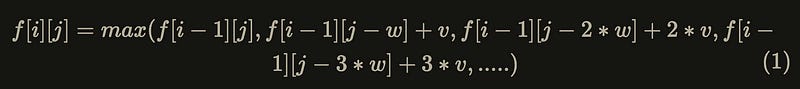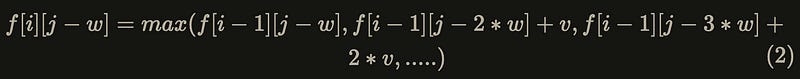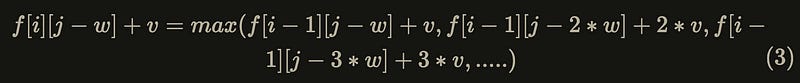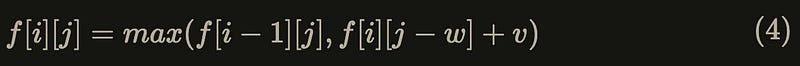Unveiling the Unbounded Knapsack Problem
The unbounded knapsack problem is an important subtopic of dynamic programming, with significant applications in many fields.
The unbounded knapsack problem is an important subtopic of dynamic programming, with significant applications in algorithm competitions and interviews.
Problem description is as follows:
There are
n(n <= N) items and a backpack with a capacity ofm(m <=M). Each item has infinite quantity. The weight and value of the i-th item arew[i]andv[i]respectively.
Now we need to select some items to put in the backpack, and the total capacity cannot exceed the capacity of the backpack. We need to find the maximum total value of the items that can be reached.
In fact, this is similar to the 0/1 knapsack problem, but each item can be selected unlimited times (within the allowed capacity).
The 0/1 knapsack problem is the core of the knapsack problem. If you are not familiar with it, you can refer to this article: 0/1 Knapsack Problem
Conventional Solution
For unbounded knapsack problem, We can directly use the definition of the 0/1 knapsack problem:
f[i][j]represents the maximum value that can be obtained by considering the firstiitems and putting them into a knapsack with capacityj.
Since each item can be selected multiple times, for a given f[i][j], its value should be the maximum value among all possible scenarios:
Maximum value of selecting i-th item 0 times:
f[i-1][j]Maximum value of selecting i-th item once:
f[i-1][j-w[i]] + v[i]Maximum value of selecting i-th item 2 times:
f[i-1][j-2*w[i]] + 2*v[i]…
…
Maximum value of selecting i-th item k times:
f[i-1][j-k*w[i]] + k*v[i]
We can obtain the state transition equation as:
Code as follows:
#include<iostream>
using namespace std;
const int N = 1e3 + 7; // Maximum quantity of items
const int M = 1e4 + 7; // Maximum capacity of the backpack
int n,m;
int f[N][M];
int v[N],w[N]; // Value and Weight of Items
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++)
cin >> w[i] >> v[i];
for(int i = 1; i <= n; i++)
for(int j = 0; j <= m; j++)
for(int k = 0; k * w[i] <= j; k++)
// Choose i-th item k times
f[i][j] = max(f[i][j],f[i-1][j - k * w[i]] + k * v[i]);
cout << f[n][m] << endl; // Output Result
return 0;
}Time complexity: We find that there are N * M states that need to be transferred, but each transfer requires enumerating the number of current items, which can be enumerated up to M times (the weight is at least 1), so the overall complexity is O(N * M * M).
Space complexity: O(N * M)
Optimization Ideas
We list the internal relationships of the update order, let v = v[i], w = w[i]:
Replace j in equation (1) with j — w:
Add v to both sides of equation (2):
It is found that equation (3) is actually the second term and beyond inside the max function on the right-hand side of equation (1). So substituting equation (3) into equation (1):
According to equation (4), the loop for iterating through k can actually be eliminated, which is a huge improvement. The optimized code looks like this:
#include<iostream>
using namespace std;
const int N = 1e3 + 7; // Maximum quantity of items
const int M = 1e4 + 7; // Maximum capacity of the backpack
int n,m;
int f[N][M];
int v[N],w[N]; // Value and Weight of Items
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++)
cin >> w[i] >> v[i];
for(int i = 1; i <= n; i++)
for(int j = 0; j <= m; j++)
{
if(j < w[i])
f[i][j] = f[i-1][j];
else
f[i][j] = max(f[i-1][j],f[i][j - w[i]] + v[i]);
}
cout << f[n][m] << endl; // Output Result
return 0;
}One-dimensional optimization
We found that this code is very similar to the two-dimensional implementation of 0/1 knapsack problem. Below is the core code for 0/1 knapsack problem:
for (int i = 1; i <= n; i++)
for (int j = 0; j <= m; j++)
{
if (j < w[i])
f[i][j] = f[i - 1][j];
else f[i][j] = max(f[i - 1][j], f[i - 1][j - w[i]] + v[i]);
}Actually, the two codes only differ in one line:
f[i][j] = max(f[i - 1][j], f[i - 1][j - w[i]] + v[i]); // 0/1 knapsack problem
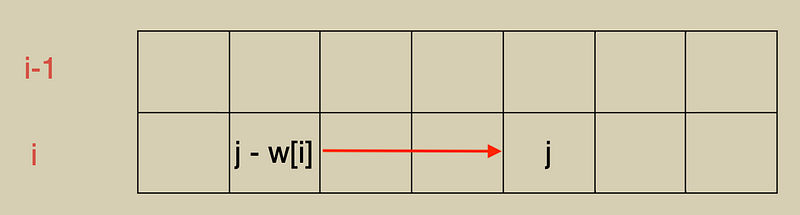
f[i][j] = max(f[i - 1][j],f[i][j - w[i]] + v[i]);// Unbounded Knapsack Problem Because it is very similar to the 0/1 knapsack code, it can be processed into one dimension, but it must be traversed in order.
The reason is that when updating f[j], f[j-w[i]] must be the value of the current row, that is, to ensure that f[j-w[i]] has been updated, so the traversal direction is from small to large.
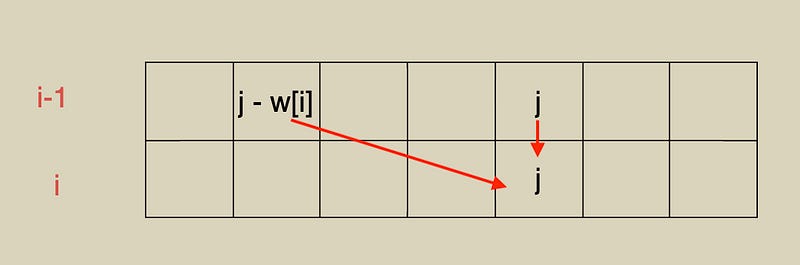
Let’s review why we have to traverse the 0/1 knapsack problem in reverse order. This is because only reverse traversal can ensure that when updating f[j], the data stored in f[j — w[i]] is from the previous row. If we traverse in order, f[j — w[i]] will be updated earlier when updating f[j], and it will no longer be the data from the previous row:
In summary, the one-dimensional implementation of the unbounded knapsack problem is as follows:
#include<iostream>
using namespace std;
const int N = 1e3 + 7; // Maximum quantity of items
const int M = 1e4 + 7; // Maximum capacity of the backpack
int n,m;
int f[M];
int v[N],w[N]; // Value and Weight of Items
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++)
cin >> w[i] >> v[i];
for(int i = 1; i <= n; i++)
for(int j = w[i]; j <= m; j++)
f[j] = max(f[j],f[j - w[i]] + v[i]);
cout << f[m] << endl; // Output Result
return 0;
}Time complexity: We find that there are N * M states that need to be transferred, so the complexity is O(N * M).
Space complexity: O(M)
Conclusion
This article describes the solutions, and optimization methods of the unbounded knapsack problem.
In the future, I will introduce some example problems related to the this Problem.
Finally, if there are any omissions or errors in this article, please kindly advise me. Thank you.