Segment Tree 1: Basic Concepts and Operations in Detail
By creating advanced data structures like segment trees ahead of time, we can perform two operations, query and update, in O(logn) time…
In computer science, segment tree is a tree data structure used for storing information about intervals as a tree.
It allows answering range queries over an array efficiently and still being flexible enough to allow quick modification of the array.
Segment tree has powerful abilities and supports operations such as finding the sum of an interval, finding maximum of an interval, updating an interval, and updating a single point.
Problem
Assuming there is a very large array, two operations need to be performed repeatedly many times on the elements of this array.
Query: Select an interval in this array and find the sum of all elements in this interval.
Update: Add a value to an element of the array.
Core idea
The concept of a segment tree is similar to divide and conquer.
To efficiently obtain the sum of the interval [l, r] (represented by s), we can divide it into two intervals [l, mid] and [mid+1, r]. If we know the sum of [l, mid] (represented by sl) and [mid+1, r] (represented by sr) in advance, we can obtain s = sl + sr directly, as shown in Figure 1:
However, we don’t know sl and sr initially, so we keep dividing the interval until the segment length is 1. At this point, we can directly get the sum of the single element on the array.
For example, to get the interval sum of [1,4], we divide it into the sum of [1,2] and [3,4], then into four intervals: [1,1], [2,2], [3,3], and [4,4].
By treating each interval as a node and its two sub-intervals as child nodes, we can construct a binary tree-like structure, called a segment tree, that maintains the sum of each interval.
Storage
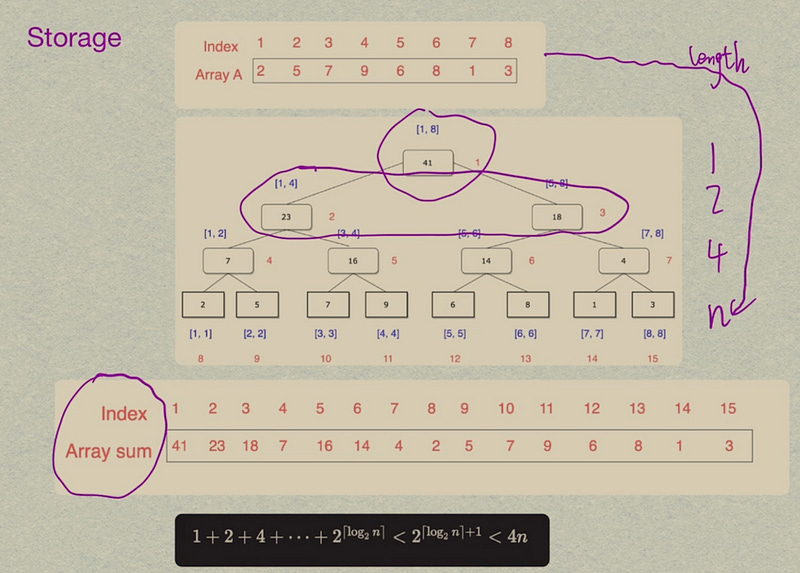
The first consideration when implementing a segment tree is how to store it in memory. One approach is to define a tree structure and create objects that store the segment boundaries, sum, and pointers to child nodes. However, this approach requires storing redundant information in the form of pointers.
To reduce storage requirements, we can use a simple trick similar to binary heaps. Instead of storing pointers, we can store only the sums in an array called “sum”. The length of this array will be discussed shortly.
The sum of the root node at index 1(That’s why the array is required to be 1-indexed), the sums of its two child nodes at indices 2 and 3, the sums of the children of those two vertices at indices 4 to 7, and so on.
With 1-indexing, conveniently the left child of a vertex at index i is stored at index 2i , and the right one at index 2i + 1 . Equivalently, the parent of a node at index i is stored at i/2 (integer division), as shown in Figure 2:
This simplifies the implementation a lot. We don’t need to store the structure of the tree in memory. It is defined implicitly. We only need one array which contains the sums of all segments.
We found that the first level of the tree contains a single node (the root), the second level contains 2 nodes, and the third level contains 4 nodes. This pattern continues until the last level, where the number of nodes reaches n (n represents the length of the array A).
Therefore, the number of nodes in the worst case can be estimated by the sum:
We can conclude that a segment tree only requires a linear number of nodes, as shown in Figure 3:
It is worth noting that whenever the length of array A is not a power of 2, not all levels of the segment tree will be completely filled. In other words, the segment tree is not necessarily a complete binary tree.
Figure 4 shows an example of a segment tree for an array with 5 elements, which is not a power of 2:
Construction
The algorithm for constructing a segment tree is as follows:
const int MAX_LEN = 1e5 + 9;
int sum[4 * MAX_LEN];
void push_up(int rt)
{
sum[rt] = sum[rt * 2] + sum[rt * 2 + 1];
}
void build(int A[], int rt, int L, int R)
{
if (L == R)
{
sum[rt] = A[L];
}
else
{
int mid = (L + R) / 2;
build(A, rt * 2, L, mid);
build(A, rt * 2 + 1, mid + 1, R);
push_up(rt);
}
}MAX_LEN is the maximum length that array A can reach. As mentioned earlier, the sum array needs to be four times the size of array A.
The build function has 4 parameters:
The original array
AThe tree node number (denoted by
rt)The left boundary of a closed interval corresponding to
rt(denoted byL)The right boundary of a closed interval corresponding to
rt(denoted byR)
We begin constructing the segment tree at the root node (numbered 1), with a left boundary of 1 and a right boundary of 8. By following a recursive process, we can construct the entire segment tree.
When the procedure is called on a non-leaf vertex, it does the following:
Recursively constructs the values of the two child vertices.
Merges the computed values of these children.
When a leaf node is reached, the condition is L = R.
For example, let’s say that l = 1 and r = 8. We can calculate mid by taking the average of l and r, which gives us (1 + 8) / 2 = 4 (rounded down). This interval can be divided into two parts: [1, 4] and [5, 8]. It’s important to note that the value of the root is currently undetermined. We will calculate it using the pushup function after we obtain the values of its two children.
The process is shown in Figure 5:
First, we go to the left child. Now,
l = 1,r = 4, and mid is(1 + 4) / 2 = 2(rounding down). This interval is divided into two parts:[1,2],[3, 4].Then we go to the left child. Now,
l = 1,r = 2, and mid is(1 + 1) / 2 = 1(rounding down). This interval is divided into two parts:[1,1],[2, 2].Then we go to the left child. Now,
l = r = 1, so we assign this node a value of2, which isa[1]in the original array.When the recursive function returns to the parent node, we go to the right child. The right child is the same as the left child, so we can assign this node a value of
5, which isa[2]in the original array.When the recursive function returns to the parent node again, after obtaining the value of all child nodes, we can easily obtain the value of the parent node, which is
2 + 5 = 7. This process is called pushup.
The construction of other nodes can also be deduced by analogy.
After construction, the segment tree is shown in figure 6:
The red font on the right side of the node represents the node number, which is also the index of the sum array. The numbers in the boxes represent the values of the sum array.
To summarize the build process:
We start at the root node and recursively descend to the bottom level (the leaf nodes) to assign them their respective values.
Based on these values, we can compute the values of the previous level using the pushup function. We can then compute the values of the previous level based on those, and repeat the procedure until we reach the root vertex.
Characteristics
Each node in the segment tree represents an interval.
The segment tree has a unique root node, which represents the entire range of the array:
[1, n].For each child node, it represents a sub-interval in the entire sequence.
For each leaf node, it represents a single element in the sequence. Each child node continuously transmits information to its parent node, which stores the integrated information of each of its sub-nodes.
For each internal node
[l, r], its left child node is[l, mid], and its right child node is[mid+1, r], wheremid=(l + r) / 2(rounded down).
Query
Once the segment tree has been constructed, the next step is to utilize this advanced data structure for efficient querying and updating. Specifically, we need to compute the sum of the interval [L, R] in O(log n) time.
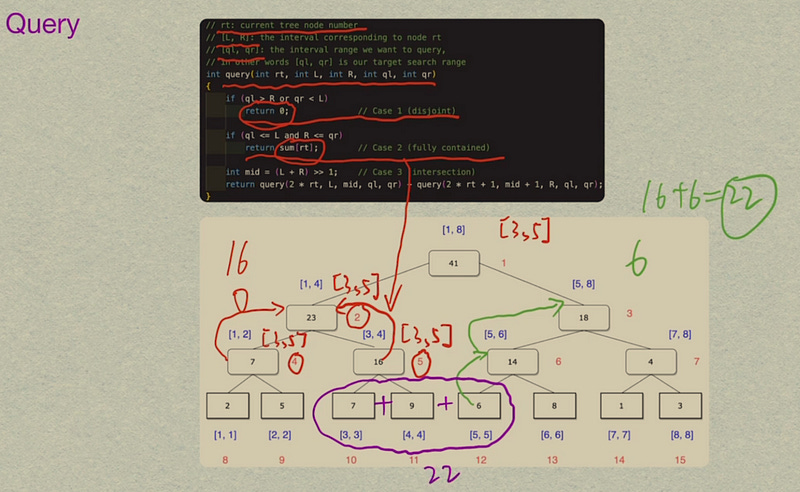
The algorithm for querying is as follows:
// rt: current tree node number
// [L, R]: the interval corresponding to node rt
// [ql, qr]: the interval range we want to query,
// in other words [ql, qr] is our target search range
int query(int rt, int L, int R, int ql, int qr)
{
if (ql > R or qr < L)
return 0; // Case 1 (disjoint)
if (ql <= L and R <= qr)
return sum[rt]; // Case 2 (fully contained)
int mid = (L + R) >> 1; // Case 3 (intersection)
return query(2 * rt, L, mid, ql, qr) + query(2 * rt + 1, mid + 1, R, ql, qr);
}The query function takes 5 parameters:
The tree node number (denoted by
rt)[L, R]represents the interval corresponding to nodert[ql, qr]represents the range we want to query, or in other words, our target search range.
To accomplish this, we traverse the segment tree and use the precomputed sums of the segments.
There are three possible cases, with Case 3 possibly containing the previous two cases:
Query: Case 1 (disjoint)
If the interval corresponding to current node rt is not within the target search range, then return 0.
Query: Case 2( fully contained )
If the interval corresponding to the current node rt is completely within the target search range, then return the sum of the interval corresponding to rt.
In this case, the interval corresponding to rt is part of our target search range, so its current interval sum can contribute to the sum of our target search range.
Query: Case 3 (intersection)
In the last case, the target search range intersects with the current interval. In this scenario, we have no other option but to make two recursive calls, one for each child.
First, we go to the left child and compute a partial answer for this node. This is the sum of values of the intersection between the segment of the query and the segment of the left child. Then, we go to the right child and compute another partial answer. Finally, we combine the answers by adding them.
For example, suppose we want to query the sum of [3, 5], the process is shown in Figure 7:
Starting from the root, we find that neither case
1nor case2are satisfied, so we make two recursive calls, one for each child.When we reach node
2, case3is satisfied, so we make two recursive calls.When we reach node
4, case3is satisfied. Since[1, 2]and[3, 5]do not intersect, we return0.When we reach node
5, case2is satisfied.[3, 4]is completely within the target search range[3, 5], so we return the interval sum of16.Thus, for the left branch of the root, we obtain
16.According to this algorithm, we obtain another part of the answer in the right branch of the root, which is
6.Finally, we add up the partial answers we obtained from the left and right subtrees. The final answer is
16 + 6 = 22. We can manually check that this is indeed the correct answer for our target search range of[3, 5].
Update
To increase A[pos] by k, we need to update the corresponding node in the Segment Tree.
Updating the tree is easier than querying it. The algorithm for updating a node is as follows:
void push_up(int rt)
{
sum[rt] = sum[rt * 2] + sum[rt * 2 + 1];
}
// rt: current tree node number
// [L, R]: the interval corresponding to node rt
// pos: the index of array A
// k: the value added to A[pos]
// The purpose of this function is to realize A[pos] += k
void update(int rt, int L, int R, int pos, int k)
{
if (L == R)
{
sum[rt] += k;
return;
}
int mid = (L + R) >> 1;
if (L <= pos and pos <= mid)
update(rt * 2, L, mid, pos, k);
if (mid + 1 <= pos and pos <= R)
update(rt * 2 + 1, mid + 1, R, pos, k);
push_up(rt);
return;
}The Update function takes 5 parameters:
The tree node number (denoted by
rt)[L, R]represents the interval corresponding to nodertposrepresents the index of arrayAkrepresents the value added toA[pos]
The goal is to locate the leaf node in the segment tree that corresponds to A[pos]. When the leaf node is updated, the value of the parent node is updated layer by layer through the push_up function.
For example, to increase A[7] by 5, we first traverse the segment tree recursively to find the leaf node corresponding to A[7], and then update its value. We update the value of the parent node when the recursive function returns to the parent node.
As shown in the Figure 8, the chain from the root to the leaf node(green circle in Figure 8) corresponding to A[7] is updated:
Time complexity
Construction: O(n), corresponding to the number of nodes in the segment tree.
Query: O(log n), as the target search range can be split into at most O(log n) intervals, and the final answer can be obtained by combining these intervals.
Update: O(log n), since each level of the segment tree forms a partition of the array, an element A[pos] only contributes to one segment from each level. Therefore, only O(log n) nodes need to be updated.
A more rigorous proof will not be provided here. Perhaps it will be elaborated on in the future.
Conclusion
This article explains the basics of segment tree, including core idea, storage, construction, characteristics, query, and single-point update.
By creating advanced data structures like segment trees ahead of time, we can perform two operations, query and update, in O(logn) time. This greatly improves efficiency.
It is worth mentioning that the Fenwick Tree (Binary Indexed Tree) is actually a subset of the Segment Tree. The advantage of the binary indexed tree is that its code is shorter, its constant is smaller, and its speed is faster.
The segment tree can maintain all operations that satisfy the associative law (such as addition, multiplication, maximum value, minimum value), and the lazy tag can also make the Segment Tree support interval modification (the next article will explain interval updates and lazy propagation for segment tree), which cannot be achieved by the binary indexed tree.
Finally, if there are any omissions or errors in this article, please kindly advise me. Thank you.