Grouped-Query Attention(GQA) Explained
From Principles to Llama2 Code Explanation
The standard practice for autoregressive decoding is to cache the keys and values of the previous tokens in the sequence to speed up attention computation. However, as the context window or batch size increases, the memory cost associated with the size of the key-value cache(kv cache) in the multi-head attention(MHA) model significantly increases.
Multi-Query attention(MQA) is a mechanism that uses only a single key-value head for multiple queries, which can save memory and greatly speed up decoder inference.
However, MQA may lead to a decrease in quality. In fact, we not only want fast inference, but also want the quality to be on par with MHA, so Grouped-query attention(GQA)[1] comes into play.
Grouped-query attention(GQA) is an interpolation of multi-query and multi-head attention. It achieves a quality similar to multi-head attention while maintaining a comparable speed to multi-query attention.
Since GQA is a newcomer, many famous large language models have not adopted it before. However, since its proposal, it has gained popularity among popular models such as Llama2[2] and Mistral 7B[3].
GQA
GQA can be seen as an intermediate or generalized form of MQA and MHA:
When there is only one group in GQA, it is referred to as MQA.
When the number of groups in GQA is equal to the number of attention heads, it is referred to as MHA.
Figure 1 provides a clear visualization of this relationship.
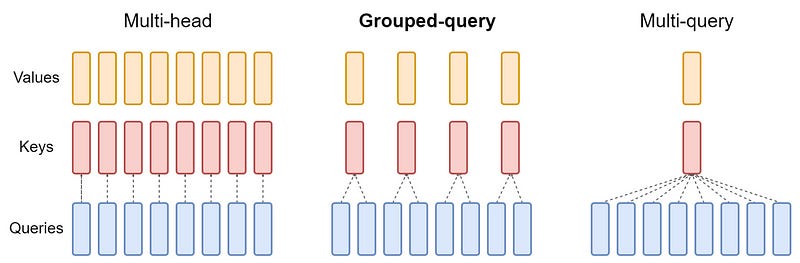
From Figure 1, it can be observed that GQA’s strategy is to enhance the inference quality by offering a modified version of MQA. This is achieved by using multiple keys and values heads but with fewer than the total number of query heads.
How to incorporate GQA into LLM
Here, let’s take a look at the approach of Llama 2. Below is the code for attention:
class Attention(nn.Module):
"""Multi-head attention module."""
def __init__(self, args: ModelArgs):
"""
Initialize the Attention module.
Args:
args (ModelArgs): Model configuration parameters.
Attributes:
n_kv_heads (int): Number of key and value heads.
n_local_heads (int): Number of local query heads.
n_local_kv_heads (int): Number of local key and value heads.
n_rep (int): Number of repetitions for local heads.
head_dim (int): Dimension size of each attention head.
wq (ColumnParallelLinear): Linear transformation for queries.
wk (ColumnParallelLinear): Linear transformation for keys.
wv (ColumnParallelLinear): Linear transformation for values.
wo (RowParallelLinear): Linear transformation for output.
cache_k (torch.Tensor): Cached keys for attention.
cache_v (torch.Tensor): Cached values for attention.
"""
super().__init__()
self.n_kv_heads = args.n_heads if args.n_kv_heads is None else args.n_kv_heads
model_parallel_size = fs_init.get_model_parallel_world_size()
self.n_local_heads = args.n_heads // model_parallel_size
self.n_local_kv_heads = self.n_kv_heads // model_parallel_size
self.n_rep = self.n_local_heads // self.n_local_kv_heads
self.head_dim = args.dim // args.n_heads
# ColumnParallelLinear and RowParallelLinear are two common strategies for implementing model parallelism.
self.wq = ColumnParallelLinear(
args.dim,
args.n_heads * self.head_dim,
bias=False,
gather_output=False,
init_method=lambda x: x,
)
# The dimension of wk and wv has changed.
self.wk = ColumnParallelLinear(
args.dim,
self.n_kv_heads * self.head_dim,
bias=False,
gather_output=False,
init_method=lambda x: x,
)
self.wv = ColumnParallelLinear(
args.dim,
self.n_kv_heads * self.head_dim,
bias=False,
gather_output=False,
init_method=lambda x: x,
)
self.wo = RowParallelLinear(
args.n_heads * self.head_dim,
args.dim,
bias=False,
input_is_parallel=True,
init_method=lambda x: x,
)
# kv cache, used for caching keys and values
self.cache_k = torch.zeros(
(
args.max_batch_size,
args.max_seq_len,
self.n_local_kv_heads,
self.head_dim,
)
).cuda()
self.cache_v = torch.zeros(
(
args.max_batch_size,
args.max_seq_len,
self.n_local_kv_heads,
self.head_dim,
)
).cuda()
def forward(
self,
x: torch.Tensor,
start_pos: int,
freqs_cis: torch.Tensor,
mask: Optional[torch.Tensor],
):
"""
Forward pass of the attention module.
Args:
x (torch.Tensor): Input tensor.
start_pos (int): Starting position for caching.
freqs_cis (torch.Tensor): Precomputed frequency tensor.
mask (torch.Tensor, optional): Attention mask tensor.
Returns:
torch.Tensor: Output tensor after attention.
"""
bsz, seqlen, _ = x.shape
# The dimension of k and v has changed.
xq, xk, xv = self.wq(x), self.wk(x), self.wv(x)
xq = xq.view(bsz, seqlen, self.n_local_heads, self.head_dim)
xk = xk.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)
xv = xv.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)
# Incorporate rotary position embedding
xq, xk = apply_rotary_emb(xq, xk, freqs_cis=freqs_cis)
self.cache_k = self.cache_k.to(xq)
self.cache_v = self.cache_v.to(xq)
# Cache current token's kv
self.cache_k[:bsz, start_pos : start_pos + seqlen] = xk
self.cache_v[:bsz, start_pos : start_pos + seqlen] = xv
# Retrieve the previously cached keys and values
keys = self.cache_k[:bsz, : start_pos + seqlen]
values = self.cache_v[:bsz, : start_pos + seqlen]
# repeat k/v heads if n_kv_heads < n_heads
# make the number of heads in kv and q the same
keys = repeat_kv(keys, self.n_rep) # (bs, cache_len + seqlen, n_local_heads, head_dim)
values = repeat_kv(values, self.n_rep) # (bs, cache_len + seqlen, n_local_heads, head_dim)
# Self-attention
xq = xq.transpose(1, 2) # (bs, n_local_heads, seqlen, head_dim)
keys = keys.transpose(1, 2) # (bs, n_local_heads, cache_len + seqlen, head_dim)
values = values.transpose(1, 2) # (bs, n_local_heads, cache_len + seqlen, head_dim)
scores = torch.matmul(xq, keys.transpose(2, 3)) / math.sqrt(self.head_dim)
if mask is not None:
scores = scores + mask # (bs, n_local_heads, seqlen, cache_len + seqlen)
scores = F.softmax(scores.float(), dim=-1).type_as(xq)
output = torch.matmul(scores, values) # (bs, n_local_heads, seqlen, head_dim)
output = output.transpose(1, 2).contiguous().view(bsz, seqlen, -1)
return self.wo(output)I have commented on the key processes of this code. There are a few points to note (assuming parallel processing is not required):
self.n_local_headsrepresents the number of heads in the original multi-head attention, also refers to the number of query heads.self.n_local_kv_headsrepresents the number of key and value heads in GQA. This means that the cache sizes for keys and values can be reduced by a factor ofself.n_rep = self.n_local_heads // self.n_local_kv_heads.Since GQA reduces the size of the KV cache, but in actual computation(matrix multiply (GEMM) subroutine), it needs to match the number of query heads. Therefore, they need to be expanded back to their original size. The
repeat_kvfunction is utilized to duplicate the keys/values and align them with the number of query heads.
def repeat_kv(x: torch.Tensor, n_rep: int) -> torch.Tensor:
"""torch.repeat_interleave(x, dim=2, repeats=n_rep)"""
bs, slen, n_kv_heads, head_dim = x.shape
if n_rep == 1:
return x # MHA
return (
x[:, :, :, None, :]
.expand(bs, slen, n_kv_heads, n_rep, head_dim)
.reshape(bs, slen, n_kv_heads * n_rep, head_dim)
) # GQA or MQALet’s take a look at an example to see what repeat_kv does:
>>> x = torch.rand(1, 1, 4, 6)
>>> x
tensor([[[[0.1898, 0.5731, 0.4586, 0.5906, 0.2105, 0.7735],
[0.6219, 0.3407, 0.3804, 0.7781, 0.3234, 0.8874],
[0.7422, 0.8980, 0.7574, 0.5109, 0.6943, 0.9066],
[0.3850, 0.7974, 0.1791, 0.6012, 0.5239, 0.4833]]]])
>>> n_rep = 2
>>> bs, slen, n_kv_heads, head_dim = x.shape
>>> print(x[:, :, :, None, :] .expand(bs, slen, n_kv_heads, n_rep, head_dim) .reshape(bs, slen, n_kv_heads * n_rep, head_dim))
tensor([[[[0.1898, 0.5731, 0.4586, 0.5906, 0.2105, 0.7735],
[0.1898, 0.5731, 0.4586, 0.5906, 0.2105, 0.7735],
[0.6219, 0.3407, 0.3804, 0.7781, 0.3234, 0.8874],
[0.6219, 0.3407, 0.3804, 0.7781, 0.3234, 0.8874],
[0.7422, 0.8980, 0.7574, 0.5109, 0.6943, 0.9066],
[0.7422, 0.8980, 0.7574, 0.5109, 0.6943, 0.9066],
[0.3850, 0.7974, 0.1791, 0.6012, 0.5239, 0.4833],
[0.3850, 0.7974, 0.1791, 0.6012, 0.5239, 0.4833]]]])
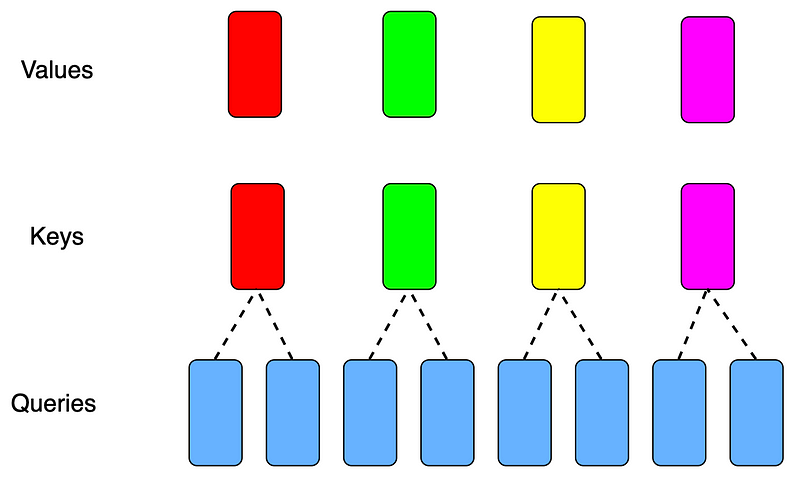
>>>To further understand the principles of GQA, I have drawn two diagrams. Figure 2 shows that the number of attention heads for keys and values is 4 (self.n_local_kv_heads = 4), and the number of attention heads for queries is 8(self.n_local_heads = 8):
As shown in Figure 3, after repeat_kv, the number of attention heads for keys and values is matched with the number of queries(each color represents a group, and the number of heads in each group has been expanded), and matrix multiply(GEMM) subroutine can be performed.
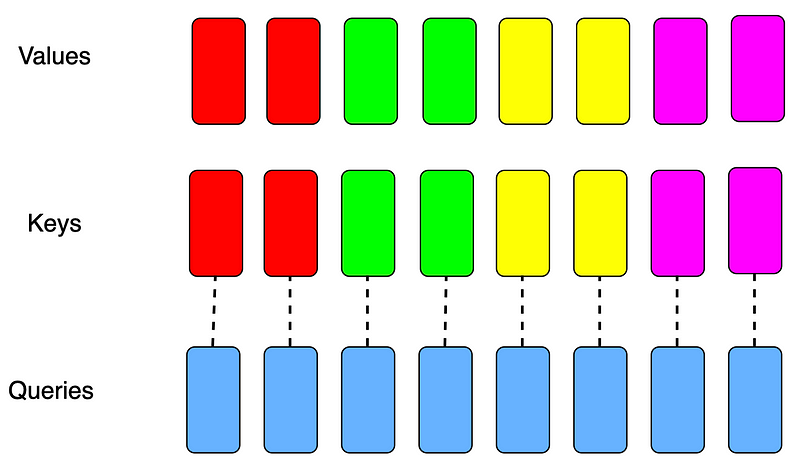
repeat_kv, the number of heads in each group has been expanded. Image by author.Conclusion
Whether it is GQA or MQA, neither of them can significantly reduce the computational load. Their main purpose is to reduce the need for storing a large amount of kv cache. As a result, the memory occupied by kv cache becomes smaller, allowing our LLM server to handle more requests, allowing for larger batch sizes and increased throughput.
Finally, if there are any errors or omissions in this text, please feel free to point them out.
References
[1]: J. Ainslie, J. Lee-Thorp, M. Jong, Y. Zemlyanskiy, F. Lebrón, S. Sanghai. GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints (2023). arXiv preprint arXiv:2305.13245.
[2]: H. Touvron, L. Martin, K. Stone, P. Albert, A. Almahairi, Y. Babaei, N. Bashlykov, S. Batra, P. Bhargava, S. Bhosale, et al. Llama 2: Open foundation and fine-tuned chat models (2023). arXiv preprint arXiv:2307.09288.
[3] A. Jiang, A. Sablayrolles, A. Mensch, C. Bamford, D. Chaplot, et al. Mistral 7B (2023). arXiv preprint arXiv:2310.06825.