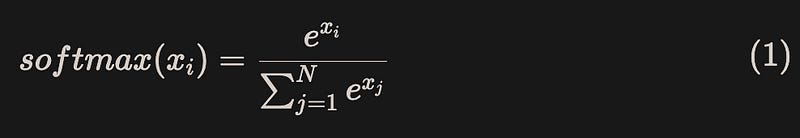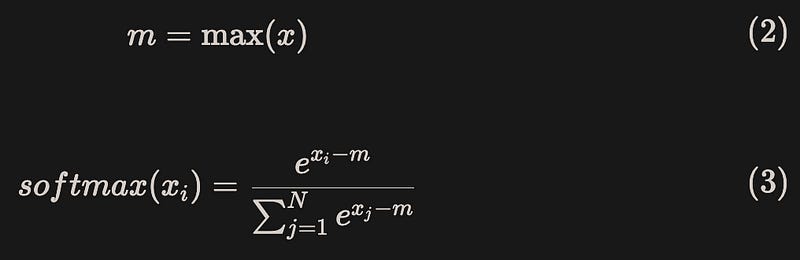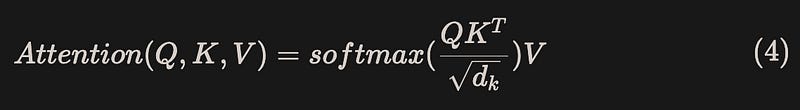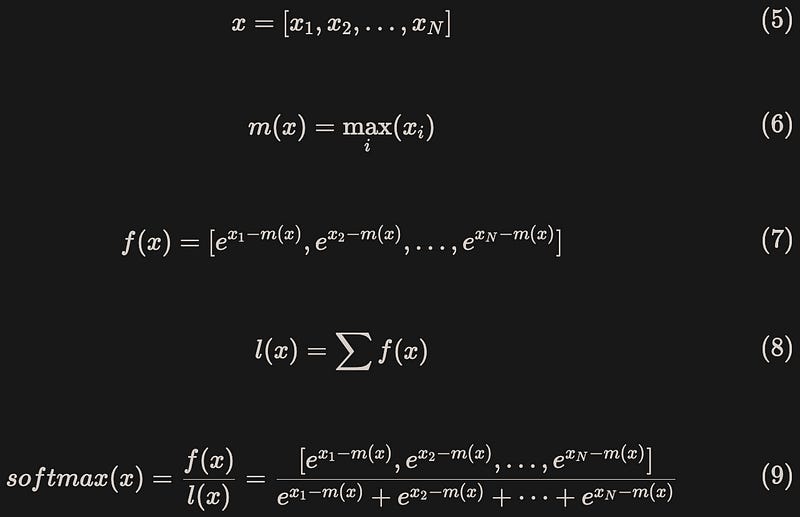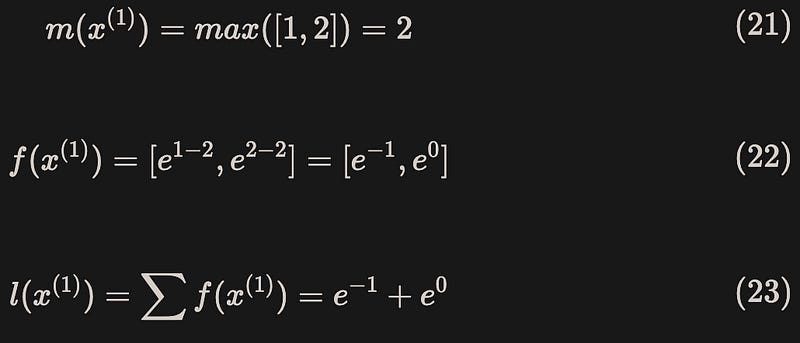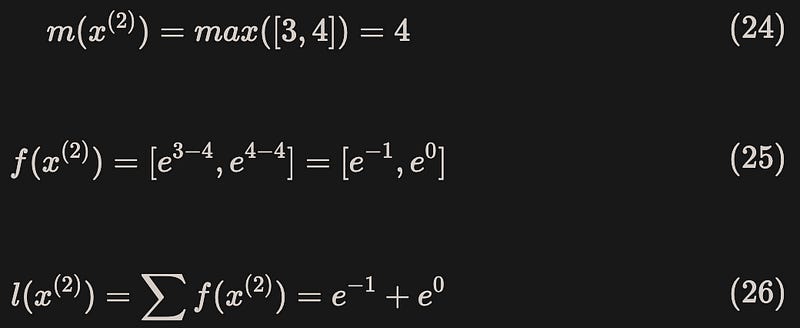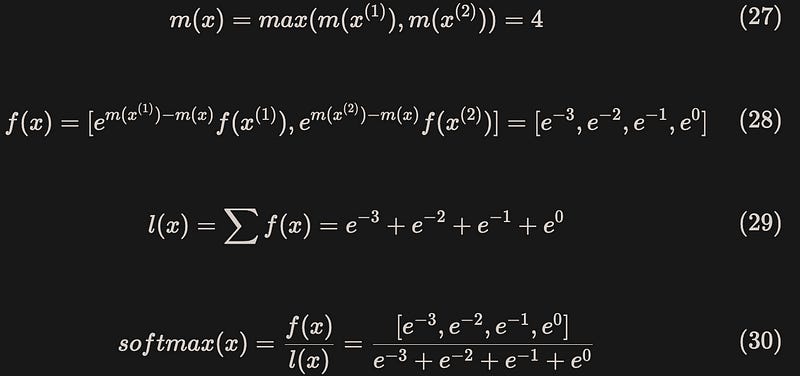Flash Attention: Underlying Principles Explained

Flash Attention is an efficient and precise Transformer model acceleration technique, this article will explain its underlying principles.

Flash Attention is an efficient and precise Transformer model acceleration technique proposed in 2022. By perceiving memory read and write operations, FlashAttention achieves a running speed 2–4 times faster than the standard Attention implemented in PyTorch, requiring only 5%-20% of the memory.

This article will explain the underlying principles of Flash Attention, illustrating how it achieves accelerated computation and memory savings without compromising the accuracy of attention.

Prerequisite Knowledge

GPU Memory Hierarchy

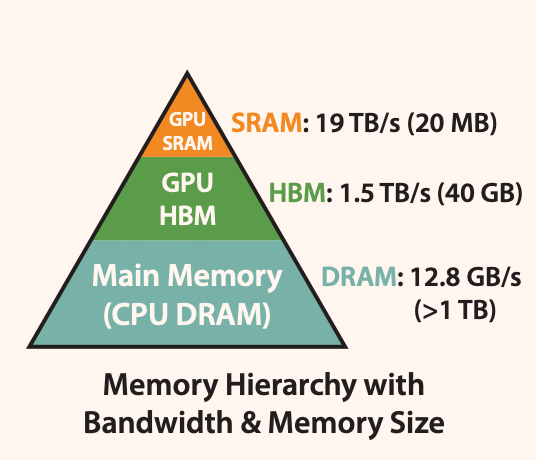
As shown in Figure 1, the memory of a GPU consists of multiple memory modules with different sizes and read/write speeds. Smaller memory modules have faster read/write speeds.

Figure 1: GPU Memory Hierarchy. Source: [1]

For the A100 GPU, the SRAM memory is distributed across 108 streaming multiprocessors, with each processor having a size of 192K. This adds up to 192 * 108KB = 20MB. The High Bandwidth Memory (HBM), which is commonly referred to as video memory, has a size of either 40GB or 80GB.

The read/write bandwidth of SRAM is 19TB/s, while HBM’s read/write bandwidth is only 1.5TB/s, less than 1/10th of SRAM’s.

Due to the improvement in computational speed relative to memory speed, operations are increasingly limited by memory (HBM) access. Therefore, reducing the number of read/write operations to HBM and effectively utilizing the faster SRAM for computation is crucial.

GPU Execution Model

GPU has a large number of threads to execute operations(called kernels). Each kernel loads inputs from HBM into registers and SRAM, performs computations, and then writes the outputs back to HBM.

Safe softmax

For x = [x1, x2, …, xN], the calculation process of naive softmax is shown in equation (1):

Equation (1): Naive softmax.

However, in actual hardware, the range of floating-point numbers is limited. For float32 and bfloat16, when x ≥ 89, the exponentiation results will become inf, causing overflow issues[3].

To avoid numerical overflow and ensure numerical stability, it is common to subtract the maximum value during calculations, known as “safe softmax”[2]:

Equation (2)-(3): Safe softmax.

Why is standard attention of Transformer slow?

The self-attention mechanism in the Transformer model allows the model to weigh different positions of the input when processing sequences, which increases the model’s representational power but also adds computational cost. Especially when dealing with long sequences, self-attention requires computing a large number of attention weights, resulting in a significant increase in time complexity.

Assuming the length of the input sequence is N, each attention head in the model needs to compute attention weights between N positions, therefore, the overall time complexity is O(N²). This means that as the sequence length increases, the computational time complexity grows quadratically, leading to slower processing speed for the model when dealing with long sequences.

For a standard Transformer model, the core Attention operation is shown in equation (4):

Equation (4): Core Attention operation.

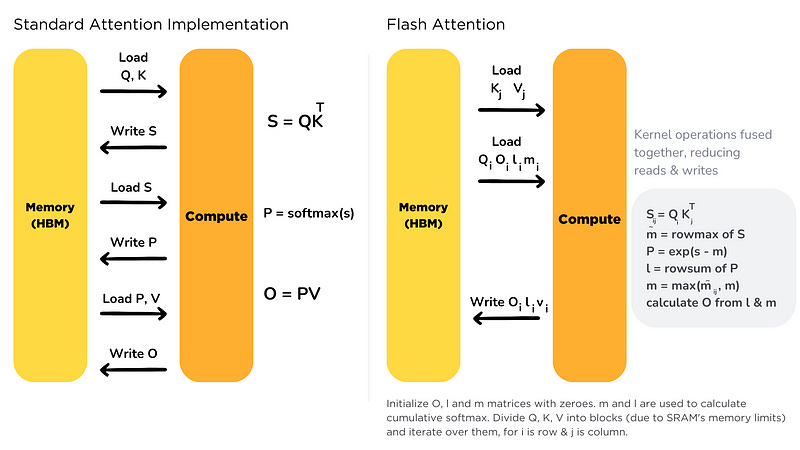
In GPU, the main computing steps are shown in Figure 2:

Figure 2: Standard attention implementation. Source: [1]

From the above process, it can be seen that the standard self-attention implementation has two issues:

• High memory usage: Instantiating the complete attention matrix S and P(dimension is N×N, N is the length of the input sequence), and writing both S and P back to HBM, consume O(N²) memory.

• Excessive read and write operations on HBM have slowed down the wall-clock time.

Improvement methods for Flash Attention

Flash Attention is improved through the following operations:

1. Tiling: The attention calculation is reconstructed by dividing the input sequence into blocks and applying the softmax operation multiple times. This method incrementally applies the softmax operation to the input blocks, reducing the computational cost. It improves computational efficiency and reduces storage requirements.

2. Recomputation: In order to avoid storing 𝑂(N²) intermediate values for the backward pass, the softmax normalization factor from the forward pass is stored during the backward propagation process, this allows for fast re-computation of attention on the chip. This method is faster than reading intermediate matrices from HBM in traditional attention methods, thus speeding up the model’s computation process.

3. At the implementation level, kernel fusion is used: From HBM, load input data and perform all calculation operations (matrix multiplication, mask, softmax, dropout, matrix multiplication) in SRAM. Then write the computation results back to HBM. The partitioned sections can be handled in a single CUDA kernel.

Tiling

From the GPU memory hierarchy shown in Figure 1, it can be observed that SRAM has a read-write speed that is one order of magnitude higher than HBM, but it has a much smaller memory size.

By fusing multiple operations into one operation through kernel fusion, calculations can be performed using the high-speed SRAM, reducing the number of HBM read-write operations and effectively reducing the runtime of memory-bound operations.

However, the memory size of SRAM is limited, and it is not possible to compute the complete attention at once. Therefore, it is necessary to perform block-wise computations, ensuring that the memory required for block-wise computations does not exceed the size of SRAM.

The difficulty in block-wise computation of attention mechanism lies in the block-wise computation of softmax. This is because when calculating the normalization factor(denominator) of softmax, it is necessary to obtain the complete input data, which makes it challenging to perform block-wise calculations.

The method of Flash Attention involves introducing two additional statistics, m(x) and l(x), to enable block-wise computation. To ensure numerical stability, the calculation process of safe softmax is shown in equation (5)-(9):

Equation (5)-(9): The calculation process of safe softmax.

Now we can divide vector x into two parts:

Equation (10)-(12): Divide vector x into two parts.

After dividing the input vector into blocks, the process of calculating safe softmax is shown in equation (13)-(20)(note that the exp function was added when calculating f(x) to ensure consistency of the results):

Equation (13)-(20): The calculation process of safe softmax(after dividing the input vector into blocks).

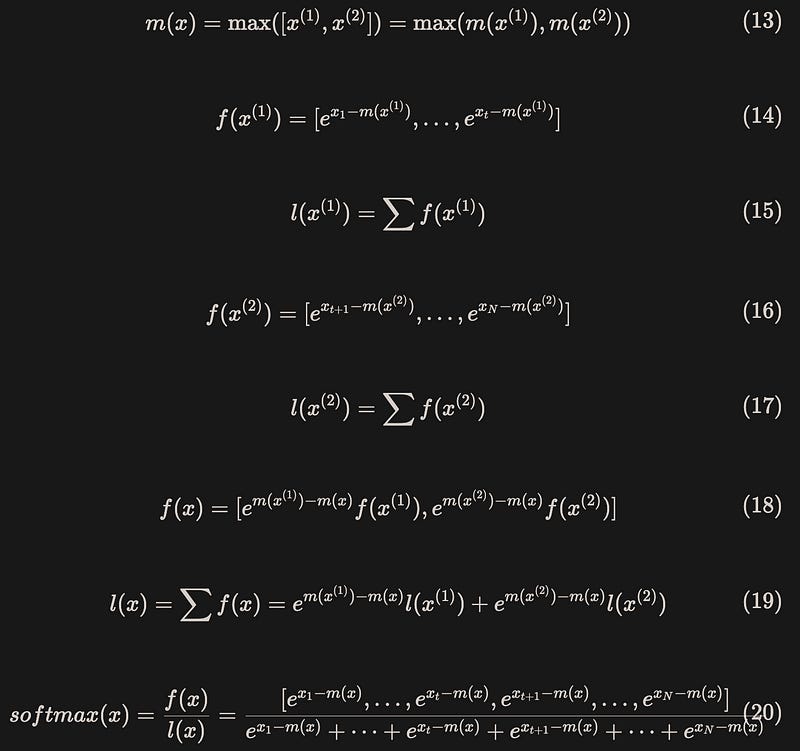
The result is exactly the same as when it is calculated without partitioning.

Below is a toy example where the vector [1,2,3,4] is split into two parts, [1,2] and [3,4], for calculation.

Block 1：

Equation (21)-(23): Block 1.

Block 2:

Equation (24)-(26): Block 2.

Merge to obtain the complete safe softmax results:

Equation (27)-(30): The complete safe softmax results.

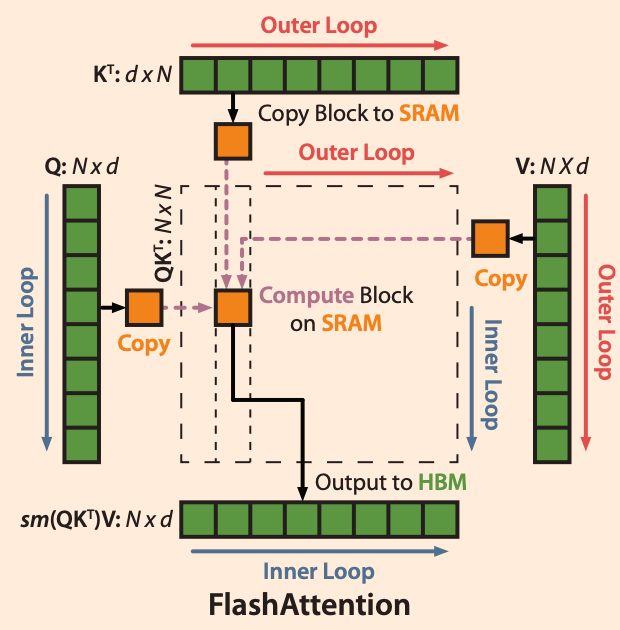
In general, the forward computation process of the Flash Attention algorithm is shown in Figure 3(line 11 represents the update process of l(x) and m(x)) and Figure 4:

Figure 3: Flash Attention algorithm. Source: [1]

Figure 4: Flash Attention uses tiling to prevent materialization of the large 𝑁 × 𝑁 attention matrix (dotted box) on (relatively) slow GPU HBM. In the outer loop (red arrows), FlashAttention loops through blocks of the K and V matrices and loads them to fast on-chip SRAM. In each block, FlashAttention loops over blocks of Q matrix (blue arrows), loading them to SRAM, and writing the output of the attention computation back to HBM. Source: [1]

Kernel fusion

Tiling technology allows us to perform all the operations of attention using a single CUDA kernel. We can load the input data from HBM and perform all the computation operations (matrix multiplication, masking, softmax, dropout, matrix multiplication) in SRAM. Then, we can write the computed results back to HBM.

By fusing multiple operations into a single operation using kernel fusion, we avoid the need for repeated data reads and writes from HBM, as shown in Figure 5[4]:

Figure 5: Kernel fusion. Source: [4]

Recomputation

In the implementation of standard attention, when calculating the gradients of Q, K, and V in the backward pass, intermediate matrices S and P of size N×N are needed, as shown in the Figure 6:

Figure 6: Standard attention backward pass. Source: [1]

Flash attention does not pre-save the two large matrices S and P. Instead, it uses a technique called recomputation. By saving two statistics m(x) and l(x), it quickly recalculates the attention matrices S and P in a block-wise manner during the backward pass on high-speed SRAM.

Compared to the standard attention method that reads a large intermediate attention matrix from HBM, it reduces the memory complexity from O(N²) to O(N). Although the re-computation adds extra computational FLOPs, overall, it runs faster and significantly reduces HBM access.

As shown in Figure 7, Flash attention requires rebuilding a block of matrix S(line 11, using Q and K) and a block of matrix P (line 13, using S and pre-saved l(x), m(x)) in order to calculate the gradients of Q, K, and V.

Figure 7: Flash Attention backward pass. Source: [1]

Performance

From the experiments in the paper, it can be seen that:

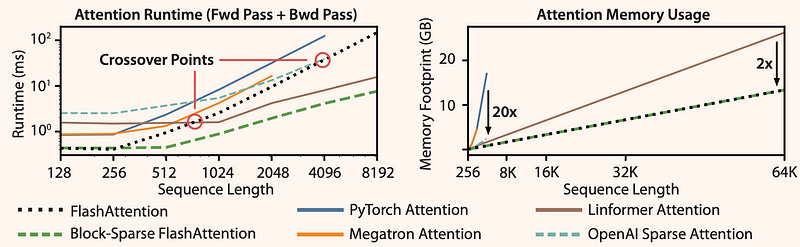
• Runtime grows quadratically with sequence length, but Flash Attention runs significantly faster than exact attention baselines, up to 3× faster than the PyTorch implementation.

• Flash Attention is up to 20× more memory efficient than exact attention baselines, and is more memory-efficient than the approximate attention baselines.

As shown in Figure 8:

Figure 8: Left: runtime of forward pass + backward pass. Right: attention memory usage. Source: [1]

Conclusion

In general, the advantages of Flash Attention are as follows:

• Accurate: Flash Attention is not an approximation, the results of Flash Attention are equivalent to standard attention.

• Fast: Flash Attention does not reduce the computational complexity in terms of FLOPs. Instead, it reduces the computation time by reducing the number of HBM accesses through IO-awareness, tiling, and kernel fusion.

• Memory-efficient: By introducing statistics and changing the computation order of the attention mechanism, Flash Attention avoids instantiating attention matrices S and P, reducing the memory complexity from O(N²) to O(N).

FlashAttention also has some limitations:

• Currently, the method of constructing IO-aware attention is to write a new CUDA kernel for each new attention implementation. This requires writing attention algorithms in a lower-level language than PyTorch and requires a lot of engineering work. The implementation may also not be transferable between GPU architectures.

• Although there has been a significant improvement in performance, it only achieves 25% to 40% of the theoretical maximum FLOPs/s of GEMM (General Matrix Multiply). This is mainly due to suboptimal task partitioning across different GPU thread blocks and warps, resulting in low utilization or unnecessary shared memory read and write operations. Therefore, Flash Attention2 has been proposed, and I will write an article to explain it.

Finally, if there are any errors or omissions in this article, please kindly point them out. Thank you.

References

[1]: T. Dao, D. Fu, S. Ermon, A. Rudra, and C. Ré. Flashattention: Fast and memory-efficient exact attention with io-awareness(2022). arXiv preprint arXiv:2205.14135.

[2]: M. Milakov, N. Gimelshein. Online normalizer calculation for softmax (2018). arXiv preprint arXiv:1805.02867.

[3]: M. Rabe, C. Staats. Self-Attention Does Not Need O(n2) Memory (2022). arXiv preprint arXiv:2112.05682.

[4]: Hugging Face. Flash Attention.