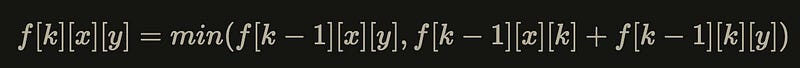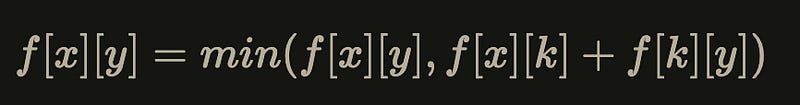Famous Algorithm with core code no more than 5 lines: Floyd-Warshall Algorithm

This article introduces the concept of the Floyd-Warshall algorithm, two typical example problems, and their corresponding solutions.

Oct 21, 2023

The Floyd-Warshall algorithm is an algorithm in graph theory used to find the shortest path between any two points. It can correctly handle directed graphs or negative-weighted shortest path problems, and is also used to calculate the transitive closure of a directed graph.

This algorithm has been simultaneously published in articles by Robert Floyd and Stephen Warshall in 1962. However, in 1959, Bernard Roy published essentially the same algorithm, but its publication went unnoticed.

The time complexity of the Floyd-Warshall algorithm is O(N³), and the space complexity is O(N²).

Perspective of dynamic programming

To describe it in simple terms, our goal is to find the shortest path from point i to point j.

Consider a graph V with vertices numbered 1 through n, we define an array f[k][x][y], which represents the shortest path length from node x to node y that only passes through nodes 1 to k (i.e., within the subgraph V’ = 1, 2, …, k, note that x and y may not be in this subgraph).

Obviously, f[n][x][y] is the shortest path length from node x to node y (since V itself is the subgraph representing the shortest path).

There are three possible values for f[0][x][y] in the initial state:

The weight of the edge between x and y (when x and y are directly connected by an edge)
0 (when x == y)
Positive infinity (when x and y are not directly connected by an edge)

Clearly, f[k][x][y] is the minimum value of the following two cases:

The shortest path that does not pass through point k: f[k-1][x][y]
The shortest path that passes through point k: f[k-1][x][k]+f[k-1][k][y]

Therefore, the state transition equation is:

We need to incrementally increase the problem size (k from 1 to n) and determine the shortest path between any two points at the current problem size:

for (k = 1; k <= n; k++)
    for (x = 1; x <= n; x++)
        for (y = 1; y <= n; y++)
            f[k][x][y] = min(f[k - 1][x][y], f[k - 1][x][k] + f[k - 1][k][y]);

We notice that the meaning of f[k][x][y] is the minimum value of all elements in the x-th row and y-th column on the plane where the first dimension is k-1. If we compress this three-dimensional matrix into a two-dimensional one, then the result f[x][y] that we want to find initially equals to the value of the original f[k-1][x][y]. It will still become the minimum value of that row and that column at the end, so changing it in place will not affect the value of the minimum.

Therefore, the first dimension has no effect on the result, and the state transition equation is changed to:

Code as follows:

for (k = 1; k <= n; k++)
    for (x = 1; x <= n; x++)
        for (y = 1; y <= n; y++)
            f[x][y] = min(f[x][y], f[x][k] + f[k][y]);

Typical example problems

Below are two typical examples that can deepen our understanding of this algorithm, from Codeforces and Leetcode.

Codeforces 295B. Greg and Graph

Due to the long description of the problem, a simplified version is provided here(the original problem link is at the end of the article) :

Given a directed weighted graph with n vertices, Greg removes vertex number x from the graph on the i-th step. When Greg removes a vertex, he also removes all the edges that go in and out of this vertex. Before executing each step, Greg wants to know the sum of lengths of the shortest paths between all pairs of the remaining vertices.

Since we are asked to find the sum of all shortest paths in the graph, we can use the Floyd-Warshall algorithm to compute all the shortest paths in the graph and then sum them up.

However, there is a requirement in the problem: at each step, we need to remove one node and compute the sum before removal.

Removing nodes seems very difficult, so we can take a reverse approach: we can look at the nodes to be removed in reverse order, which means we add them one by one.

In other words, if all the nodes to be removed have been removed, we add the last node and then compute the sum according to the problem requirement. We can repeat this process for all the nodes to be removed.

The code is as follows:

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

const int N = 507;

int n;
int to_del[N];
int f[N][N];
bool in_graph[N];       // record if one point is in the graph
ll res[N];

int main()
{
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    cin >> n;

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            cin >> f[i][j];

    for (int i = 1; i <= n; i++)
        cin >> to_del[i];
 
    for (int cur = n; cur >= 1; cur--)
    {
        int k = to_del[cur];       // current point k
        in_graph[k] = true;        // add the current point to the graph

        // Floyd-Warshall
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                if (i != j)
                {
                    f[i][j] = min(f[i][j], f[i][k] + f[k][j]);
                    // it only makes sense when both i and j are in the graph
                    if (in_graph[i] and in_graph[j])
                        res[cur] += f[i][j];// answer in current deletion process
                }
    }

    for (int i = 1; i <= n; i++)
        cout << res[i] << ' ';      // output result
    cout << endl;

 return 0;
}

Leetcode 2642. Design Graph With Shortest Path Calculator

Due to the long description of the problem, a simplified version is provided here(the original problem link is at the end of the article) :

There is a directed weighted graph that consists of n nodes numbered from 0 to n - 1. The edges of the graph are initially represented by the given array edges where edges[i] = [fromi, toi, edgeCosti] meaning that there is an edge from fromi to toi with the cost edgeCosti.

Implement the Graph class:

Graph(int n, int[][] edges) initializes the object with n nodes and the given edges.

addEdge(int[] edge) adds an edge to the list of edges where edge = [from, to, edgeCost]. It is guaranteed that there is no edge between the two nodes before adding this one.

int shortestPath(int node1, int node2) returns the minimum cost of a path from node1 to node2. If no path exists, return -1. The cost of a path is the sum of the costs of the edges in the path.

The difficulty of this problem is Hard, but the approach is relatively straightforward:

Initialization: Use the Floyd-Warshall algorithm to find the shortest path between each pair of points (i, j) and store it in f[i][j]. This takes O(n³) time.
addEdge(x, y, w): If w >= f[x][y], then there is no need to update the shortest path for any pair of points. Otherwise, for each pair of points (i, j), update f[x][y] = min(f[x][y], f[i][x] + f[y][j] + w). The time complexity of addEdge is O(n²).
To query the shortest path between node1 and node2, it only takes O(1) time.

The code is as follows:

const int INF = 0x3f3f3f3f;

class Graph {
public:
    int n, f[400][400];

    Graph(int n_, vector<vector<int>>& edges) {
        memset(f, 0x3f, sizeof(f));   // Initialize to a large value
        n = n_;
        for(int i = 1; i <= n; i++)
            f[i][i] = 0;

        for(int i = 0; i <= (int)edges.size() - 1; i++)
            f[edges[i][0] + 1][edges[i][1] + 1] = edges[i][2];  // 1-indexed

        // Floyd-Warshall algorithm
        for(int k = 1; k <= n; k++)
            for(int i = 1; i <= n; i++)
                for(int j = 1; j <= n; j++)
                    f[i][j] = min(f[i][j], f[i][k] + f[k][j] );
    }
    
    void addEdge(vector<int> edge) {
        int x = edge[0] + 1, y = edge[1] + 1, w = edge[2];  // 1-indexed
        if (w >=  f[x][y])
            return;
        
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= n; j++)
                f[i][j] = min(f[i][j], f[i][x] + f[y][j] + w);
    }
    
    int shortestPath(int node1, int node2) {
        int x = node1 + 1, y = node2 + 1;     // 1-indexed
        if (f[x][y] != INF)
            return f[x][y];
        else
            return -1;
    }
};


/**
 * Your Graph object will be instantiated and called as such:
 * Graph* obj = new Graph(n, edges);
 * obj->addEdge(edge);
 * int param_2 = obj->shortestPath(node1,node2);
 */

Conclusion

This article introduces the concept of the Floyd-Warshall algorithm, two typical example problems, and their corresponding solutions.

The Floyd-Warshall algorithm is applicable to many types of graphs, whether they are directed or undirected, with positive or negative edge weights, but the condition is that the shortest path must exist, that is, there cannot be a negative cycle.

Finally, if there are any errors, please kindly provide feedback. Thank you.

Reference

https://en.wikipedia.org/wiki/Floyd%E2%80%93Warshall_algorithm

https://cp-algorithms.com/graph/all-pair-shortest-path-floyd-warshall.html

https://codeforces.com/problemset/problem/295/B

https://leetcode.com/problems/design-graph-with-shortest-path-calculator/

AI Exploration Journey

Discussion about this post