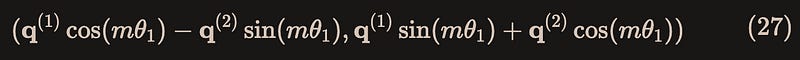An In-depth exploration of Rotary Position Embedding (RoPE)
Including principles, visual illustrations, and code
Rotary Position Embedding (RoPE)[1] is a widely used positional encoding technique, which is utilized by many large language models such as Llama[2], Llama2[3], PaLM[4], CodeGen[5], and more.
Recently, I have carefully studied the paper[1] on RoPE and derived its formulas. I would like to share them here in the hope of helping readers understand this clever idea.
This article mainly consists of three parts, including an introduction to the underlying principles, visual illustrations, and an analysis of the RoPE code in the Llama model.
Why do we need a positional encoding technique?
The Transformer model owes its remarkable performance to the essential Attention mechanism, which calculates the attention weights between each token in the input sequence.
Let’s assume a sequence has N tokens. The embeddings of the m-th token is xm, and the embeddings of the n-th token is xn.
Without adding position information to the word embeddings, we can transform them into queries qm, keys kn, and values vn as shown in equation (1):
The queries and keys are then used to compute the attention weights, while the output is computed as the weighted sum over the values, as shown in equation (2):
We discovered that when positional information is not included, the attention weight a(m, n) between tokens xm and xn remains constant regardless of their positions. In other words, the attention weight a(m, n) is position-independent, which goes against our intuition. For instance, the meanings of “dog bites cat” and “cat bites dog” are clearly distinct.
Furthermore, when two tokens are closer in distance, we expect the attention weight between them to be larger. Conversely, when the distance is greater, the attention weight should be smaller.
To resolve this issue, we can introduce positional encoding to the model. This allows each word embedding to incorporate information about its position in the input sequence. We define a function f to incorporate positional information m into word embedding xm, resulting in qm. Similarly, we incorporate positional information n into word embedding xn, resulting in kn and vn, as shown in equation (3):
After incorporating the position information, we can substitute equation (3) into equation (2) to introduce the position information in the attention mechanism. This is particularly important for tasks that are sensitive to position, such as NER (Named Entity Recognition).
Core Idea of Rotary Position Embedding (RoPE)
RoPE aims to incorporate relative position information (m — n) into the inner product of qm and kn in equation(3).
How can we determine if it contains position information? It is sufficient to represent the inner product of qm and kn as a function g(xm, xn, m-n) of xm, xn, and m-n, where m-n represents the relative position information between the two vectors. Therefore, our modeling objective becomes finding a function f that satisfies the following equation(4):
In the attention mechanism, the interaction between tokens is implied in the dot product operation between query and key. If we define the dot product of qm and kn as a function of m-n, we can assign position information to each token by implementing absolute positional encoding using function f.
How does RoPE find a function f that satisfies the conditions
Currently, the only known information is equation (3) and (4), and nothing else is known.
Finding a function f that satisfies a given condition is not an easy task in the vast space of functions. A common approach when facing a difficult problem is to try to simplify it. First, consider the case of simplicity and clarity, and then generalize it to more complex situations.
Step 1: Simplify the problem by assuming that the embedding dimension is 2.
The embedding dimension of LLMs is certainly much larger than 2, but we can generalize from this simple case.
In the 2D case, qm and kn are two-dimensional vectors. For a 2D vector, we can view it as a complex number on the complex plane. Therefore, qm and kn can be written in the form of complex numbers with their respective modulus and argument. Similarly, we can also express the inner product function g in the form of complex numbers, where R and Θ represent the modulus and argument respectively. This yields equation (5):
Step 2: Substituting equation (5) into equation (4)
We can obtain the following relationship:
Step 3: Calculate the modulus of function f based on equation (6)
For equation (6), let m = n, we obtain equation (8):
The reason why the second equal sign in Equation (8) holds is that for Equation (6), we can set m = n = 0.
Equation (8)’s final equality holds true due to the initial conditions (m = 0, n = 0) of equation (5), as shown in equation (9):
From equation (8), it can be seen that the modulus of function f is only related to the modulus of qm and kn, and is independent of the value of m. Therefore, let’s give a solution directly using the simplest relationship:
In this way, the modulus of function f is obtained. Next, we need to find the argument of the function f.
Step 4: Determine the argument of function f based on equation (7)
For equation (7), by setting m = n, we obtain equation (11):
The reason why the second equal sign in equation (11) holds is because for equation (7), we can set m = n = 0.
Equation (11)’s final equality holds true due to equation(9).
Rearrange according to equation (11):
Observing equation (12), it explains an important problem. The values on both sides of equation (12) are only related to m and are independent of x. Whether x = xm or x = xn, it remains the same. The left side of equation (12) can be denoted as:
Observing the relationship between ϕ(m+1) and ϕ(m):
It can be seen that ϕ(m) is a function of m, while the value of ϕ(m+1) — ϕ(m) is independent of m. This indicates that ϕ(m) should be an arithmetic sequence with respect to m :
It can be seen that step 4 is to prove that {ϕ(m)} is an arithmetic sequence.
Step 5: Finding the function f
Combining equations (10) and (15), we find that the modulus and argument of the function f have already been determined, which means we have found the function f.
Specifically, substituting equation (15) (for simplicity, setting γ = 0) and equation (10), (13) into equation (5):
Step 6: Determine q and the final result
A typical choice[6][7] of equation (3) is:
where pm is a vector depending of the position of token xm .
Recalling the definition of q in equation (9), it is defined for the case when m = 0. Here, we assume that there is no position information when m = 0, and this is also done to be compatible with equation (17). We directly define it as:
So the final result is:
We can substitute equation (19) into equation (10) to verify that it also holds true. Interested readers can calculate it themselves.
Write equation (19) in the form of a 2D matrix, where Wq is a 2x2 matrix, xm and q are 2D vectors:
This is a vector rotation function, which means that by rotating the vector by an angle mθ, we can add absolute positional information to the vector. This is the origin of rotational position encoding. It is amazing how beautiful mathematics can be.
Visual Representation
To gain a better understanding of positional encoding in RoPE, the following description combines graphics to illustrate how to assign positional encoding to a two-dimensional embedding.
Assuming a 2D embedding q = (1, 0), and the θ in equation(20) is a constant, let’s assume θ = 1 in this case. When the token is located at position m = [0, 1, 2, 3, 4, 5], corresponding positional information can be assigned to it, as shown in Figure 1:
Promotion to high-dimensional space
The previous content introduced how to assign position information to a two-dimensional vector, which can be achieved by rotating a certain angle. However, in practice, the dimensions of embeddings are usually in the hundreds or even thousands. Now, the question is how to extend the two-dimensional case to multiple dimensions.
The approach presented in the paper is quite straightforward. Typically, embedding dimensions are even numbers. Therefore, we decompose the high-dimensional vectors into pairs and rotate them individually. The rotation of the high-dimensional vectors can be represented as the following equations:
Here θ are all constants, and in the paper, they are directly assigned values, the inspiration may come from sinusoidal position encoding[6]:
where d is the embedding dimension.
Figure 2 shows the approach to dealing with high-dimensional situations:
RoPE Implementation in Llama
The following code snippets are all from the same file. I have added comments at the key code section.
precompute_freqs_cis function
def precompute_freqs_cis(dim: int, end: int, theta: float = 10000.0):
"""
Precompute the frequency tensor for complex exponentials (cis) with given dimensions.
This function calculates a frequency tensor with complex exponentials using the given dimension 'dim'
and the end index 'end'. The 'theta' parameter scales the frequencies.
The returned tensor contains complex values in complex64 data type.
Args:
dim (int): Dimension of the frequency tensor.
end (int): End index for precomputing frequencies.
theta (float, optional): Scaling factor for frequency computation. Defaults to 10000.0.
Returns:
torch.Tensor: Precomputed frequency tensor with complex exponentials.
"""
# Each group contains two components of an embedding,
# calculate the corresponding rotation angle theta_i for each group.
freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
# Generate token sequence index m = [0, 1, ..., sequence_length - 1]
t = torch.arange(end, device=freqs.device) # type: ignore
# Calculate m * theta_i
freqs = torch.outer(t, freqs).float() # type: ignore
freqs_cis = torch.polar(torch.ones_like(freqs), freqs) # complex64
return freqs_cispThis function is still quite abstract. Let me give an example to illustrate it, when dim = 4(the embedding dimension is 4) and the sequence length is 3, the generated freqs_cis would be:
tensor([[ 1.0000+0.0000j, 1.0000+0.0000j],
[ 0.5403+0.8415j, 0.9999+0.0100j],
[-0.4161+0.9093j, 0.9998+0.0200j]])You can see in equation(25):
freqs_cishas3components, corresponding to a sequence length of3.Each component is composed of two complex numbers.
Why is it necessary to calculate this form in advance, you will see in the apply_rotary_emb function below.
apply_rotary_emb function
The function is to apply RoPE to input tensors. It first reshapes xq into two components per group, and then converts it into complex form as xq_.
xq_ is then multiplied with freqs_cis using multiplication of complex numbers.
def apply_rotary_emb(
xq: torch.Tensor,
xk: torch.Tensor,
freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:
"""
Apply rotary embeddings to input tensors using the given frequency tensor.
This function applies rotary embeddings to the given query 'xq' and key 'xk' tensors using the provided
frequency tensor 'freqs_cis'. The input tensors are reshaped as complex numbers, and the frequency tensor
is reshaped for broadcasting compatibility. The resulting tensors contain rotary embeddings and are
returned as real tensors.
Args:
xq (torch.Tensor): Query tensor to apply rotary embeddings.
xk (torch.Tensor): Key tensor to apply rotary embeddings.
freqs_cis (torch.Tensor): Precomputed frequency tensor for complex exponentials.
Returns:
Tuple[torch.Tensor, torch.Tensor]: Tuple of modified query tensor and key tensor with rotary embeddings.
"""
# Reshape and convert xq and xk to complex number
xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))
xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))
freqs_cis = reshape_for_broadcast(freqs_cis, xq_)
# Apply rotation operation, and then convert the result back to real numbers.
xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3)
xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)
return xq_out.type_as(xq), xk_out.type_as(xk)To explain the reason for using multiplication with complex numbers, let’s looking back at the previous high-dimensional rotation matrix(equation (23)), the rotation matrix is decomposed into d/2 groups, with each group containing only two components. Here, let’s take the example of d = 4.
For the 4-dimensional case, the calculation method of apply_rotary_emb is as follows: the multiplication of complex numbers is performed between the red boxes, and the multiplication of complex numbers is also performed between the green boxes. The complex form of the rotation matrix is provided by the pre-calculated freqs_cis, and the complex form of q is provided by xq_.
Why does the multiplication of complex numbers work?
As shown in Figure 3, this is because the multiplication result between the red boxes is given by(without loss of generality, let’s take the red box as an example here) equation(27):
The complex form of equation(27) is obtained by multiplying the following two complex numbers provided respectively by xq_ and pre-calculated freqs_cis:
Similarly, the multiplication of complex numbers between the green boxes yields the last two dimensions of the first token’s qm. When combined with Equation (27), it forms the query embeddingqm of the first token, as shown in equation(29):
It can be seen that precompute_freqs_cis and apply_rotary_emb cleverly achieve high-dimensional RoPE position encoding by complex operations and the conversion between complex and real numbers.
Attention:: forward
Then, use apply_rotary_emb to calculate RoPE in the forward function of the Attention class.
class Attention(nn.Module):
"""Multi-head attention module."""
...
...
def forward(
self,
x: torch.Tensor,
start_pos: int,
freqs_cis: torch.Tensor,
mask: Optional[torch.Tensor],
):
"""
Forward pass of the attention module.
Args:
x (torch.Tensor): Input tensor.
start_pos (int): Starting position for caching.
freqs_cis (torch.Tensor): Precomputed frequency tensor.
mask (torch.Tensor, optional): Attention mask tensor.
Returns:
torch.Tensor: Output tensor after attention.
"""
bsz, seqlen, _ = x.shape
xq, xk, xv = self.wq(x), self.wk(x), self.wv(x)
xq = xq.view(bsz, seqlen, self.n_local_heads, self.head_dim)
xk = xk.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)
xv = xv.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)
# Calculate RoPE
xq, xk = apply_rotary_emb(xq, xk, freqs_cis=freqs_cis)
...
...Conclusion
It is worth mentioning that RoPE was proposed in 2021 when its application was not as widespread. For example, Transformer used sinusoidal position encoding[6], and later the representative model BERT used learnable position embedding[7].
When RoPE-based large models like Llama became widely used that it was discovered that RoPE could extrapolate position encoding beyond the pre-training length by using rotation matrices. This improves the model’s generalization ability and robustness, which is not possible with previous position encoding methods. As a result, RoPE has been widely applied.
Overall, RoPE cleverly applies the idea of rotating vectors to position encoding in large language models, and it is implemented using complex operations. It is a shining example of mathematical thinking in the field of artificial intelligence.
Finally, if there are any errors or omissions in this article, please do not hesitate to point them out.
References
[1]: J. Su, Y. Lu, S. Pan, A. Murtadha, B. Wen, Y. Liu. Roformer: Enhanced transformer with rotary position embedding (2021). arXiv preprint arXiv:2104.09864.
[2]: H. Touvron, T. Lavril, G. Izacard, X. Martinet, M. Lachaux, T. Lacroix, B. Rozière, N. Goyal, E. Hambro, F. Azhar, et al. Llama: Open and efficient foundation language models (2023). arXiv preprint arXiv:2302.13971.
[3]: H. Touvron, L. Martin, K. Stone, P. Albert, A. Almahairi, Y. Babaei, N. Bashlykov, S. Batra, P. Bhargava, S. Bhosale, et al. Llama 2: Open foundation and fine-tuned chat models (2023). arXiv preprint arXiv:2307.09288.
[4]: A. Chowdhery, S. Narang, J. Devlin, M. Bosma, G. Mishra, H. Chung, C. Sutton, S. Gehrmann, P. Schuh, et al. PaLM: Scaling language modeling with Pathways (2022). arXiv preprint arXiv:2204.02311.
[5]: E. Nijkamp, B. Pang, H. Hayashi, L. Tu, H. Wang, Y. Zhou, S. Savarese, C. Xiong. Codegen: An open large language model for code with multi-turn program synthesis (2022). arXiv preprint arXiv:2203.13474.
[6]: A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. Gomez, L. Kaiser, I. Polosukhin. Attention is all you need (2017). arXiv preprint arXiv:1706.03762.
[7]: J. Devlin, M. Chang, K. Lee, K. Toutanova. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding (2019). arXiv preprint arXiv:1810.04805.